Ranter
Join devRant
Do all the things like
++ or -- rants, post your own rants, comment on others' rants and build your customized dev avatar
Sign Up
Pipeless API

From the creators of devRant, Pipeless lets you power real-time personalized recommendations and activity feeds using a simple API
Learn More
Comments
-
@irene I can try that, but I'm not sure it will help.
Processes are probably killed by the OS as safety mechanism if they are too memory consuming. My python script was consuming 125GB before it was k-9'd. -
10e6 edges doesn't sound like much. 10e6 points could be different because that might be 10e12 edges. But with 10e6 edges and 1 kB data per edge, that's still only 1 GB.
Sounds like a software problem that is taking O(n^2) memory at some point, and for big data, you first don't do that and second slice the problem. -
@irene Yeah, with graphs of 1.2 million edges, and algorithms with high space (and time) complexity, apparently you can reach that 😂
-
Generally large datasets require streaming.
That's a problem with graphs though, you usually need the entire thing.
Perhaps it's your representation that's an issue, or the algorithm you're using to process it doesn't scale very well in space complexity?
As a last resort I would look for ways of partitioning the graph into digestible chunks for your algorithm. Generally that involves making some tradeoffs in accuracy etc. -
@Fast-Nop I have 250K nodes, about 5 edges per node. I tried to use nx.draw(graph) which fails, and tried to compute things like pagerank, which also fails
How do I slice the analysis to small parts? -
@RememberMe Yeah, I was wondering how to break the graph into chunks, without losing important information. This is our bloody first HW in the course. It was just theoretical blah-blah so far, without any practical tips about how to execute it on reasonable hardware.
-
@NickyBones 250e3 nodes, so the most straight-forward implementation would be a matrix with 62.5e9 entries. That works with small graphs, but not for big ones, that's probably where the n^2 bug is.
The matrix will be a sparse matrix, so you don't allocate a big array for that, but instead some sort of list per node.
Problem slicing would depend on the algorithm, and whether it's possible to use some divide and conquer strategy. -
@Fast-Nop We were shown in class how to use the networkx library, with a nice tiny set of GoT characters where everything worked perfectly.
I'm supposed to analyze the data with networkx, not write anything on my own.
I will see if they have any divide and conquer methods implemented there. -
@NickyBones that's a very sparse graph indeed, make sure your library is using a sparse representation (adj lists etc) instead of the usual dense graph thing (adj matrix etc.). If you know all the things have exactly 5 edges then you could have a custom representation that's even faster by hardcoding 5 into it somewhere but that's a lot of work.
Dunno much about page rank, one trick I used for reducing nodes was to cluster nodes and then merge similar ones. But cluster and merge are both pretty difficult to do as well and extremely sensitive to the problem at hand.
Edit: just read your latest comment, sorry, don't know anything about networkx. I programmed everything from scratch (which is probably why it was so terrible) -
@NickyBones I don't know networkx, but googling for the keywords 'networkx sparse matrix' gets quite some hits, so there could be a way forward.
-
@RememberMe I am used to programming everything from scratch so I know exactly which bugs I'm causing. I hate this "stumbling in the dark" feeling I get when working with super complicated and layered external libraries.
I'm gonna try the most common engineering trick - randomly sample from the graph to get a reduced one 😂 -
@Fast-Nop I found some threads about networkx performance issues and how to bypass it. I'll look into sparse matrix representation, thanks!
-
You might wanna look for separate trees so you can partition the whole set to a tree of trees? There are a bunch of partitioning methods tho.
-
@NickyBones oh boy that sounds dangerous, let me know how it goes xD
Generally though, partitioning algorithms basically mean clustering your graph somehow. If you can isolate nodes into pockets that influence each other a lot and don't influence others much, you got clusters that you can process independently.
Also the "shapes" of connectivity. Eg. If it's a social network then you can find relevant subgraphs using a clique-finding algorithm with a given clique size (basically a clique is a subgraph that's fully connected, i.e. if it's a social network then a bunch of people who all know each other). Still intensive as fuck but you can hopefully process the subgraphs individually then. -
@NickyBones I wonder if setting swappiness to 100 would avoid getting killed. Also you can malloc lots of ram but get killed when you actually use it (not that you do it manually with python). Also experimenting with zram could be interesting.
Does the school have some servers you can use? -
@RememberMe What is the complexity of searching for cliques? I will try that and see if
the laptop holds.
I didn't do crazy subsampling, just a factor of 10.
Histograms and such looks pretty much the same.
To get a more solid estimation, I'd have to runs everything a few times with different randomizations and look at the average. Random sampling works okish for minhash - I trust the hash -
@electrineer I'm not sure. You can get access to the super computing center for very specific and unique projects, but otherwise I don't think so.
-
@irene either that or the script has just allocated that amount and not actually tried to use it all at the same time.
Do you even have that amount of free disk space -
 sagar131015yIn one if my projects, my lead used janus graph for building graphs. He was happy with the performance but then again he had a cluster of 6 nodes each with 24gb RAM in it. His graph also had more than 10M edges (as far as I remember). You can give it a shot and see if it scales better than networkx. If you have 125G of ram, I am pretty sure it will work for 1M edges
sagar131015yIn one if my projects, my lead used janus graph for building graphs. He was happy with the performance but then again he had a cluster of 6 nodes each with 24gb RAM in it. His graph also had more than 10M edges (as far as I remember). You can give it a shot and see if it scales better than networkx. If you have 125G of ram, I am pretty sure it will work for 1M edges
Related Rants



 No questions asked
No questions asked As a Python user and the fucking unicode mess, this is sooooo mean!
As a Python user and the fucking unicode mess, this is sooooo mean!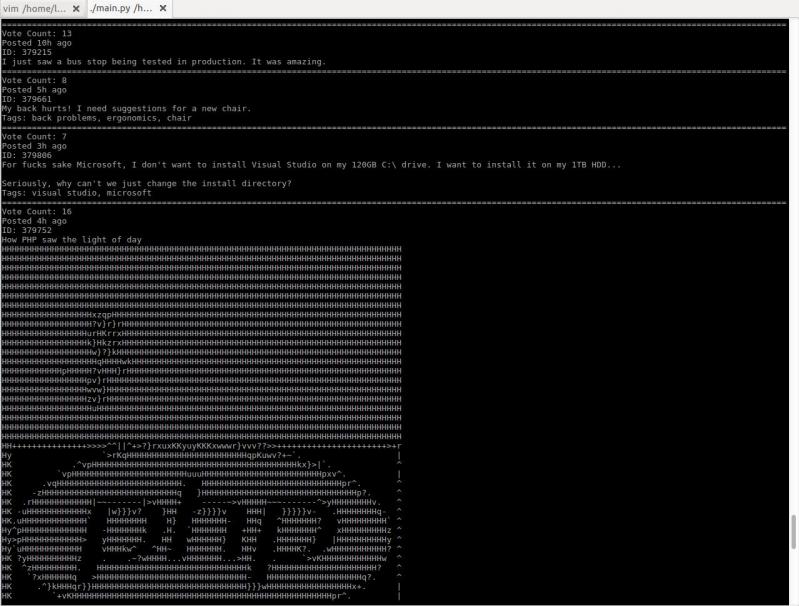 I just started working on a little project to browse devrant from terminal. It converts images to ascii art!
I just started working on a little project to browse devrant from terminal. It converts images to ascii art!
Data scientist and related devs, how do you handle large datasets?
I was given a .txt file containing +1M edges of a directed graph. I tried to analyze it with networkx, but my computer killed the process as it was eating too much CPU/memory.
I would be grateful for any advice!
rant
data science
python
networkx
dataset
pandas