Ranter
Join devRant
Do all the things like
++ or -- rants, post your own rants, comment on others' rants and build your customized dev avatar
Sign Up
Pipeless API

From the creators of devRant, Pipeless lets you power real-time personalized recommendations and activity feeds using a simple API
Learn More
Comments
-
1: To establish a big-Oh behaviour for f(n), i.e. asymptotical behaviour for n going towards infinity.
2: It is a constant multiplied with g(n). What it means is that you ignore constant factors for the big Oh behaviour. What's relevant is the scaling, not the absolute runtime.
3: Exmaining the scaling behaviour of different algorithms, or understanding hidden performance bugs with O(n²), i.e. accidental quadratic complexity.
Ever opened a shitty file explorer in a directory with some ten thousand files and watch it grinding to a halt? There is no reason why the complexity should grow more than linear, i.e. O(n) for pure display, or O(n log n) with any kind of sorted display. It grinds to a halt because someone has introduced some O(n²) behaviour. -
@Fast-Nop in addition, just want to point out that big-Oh only tells you how something *scales* based on some other quantity (usually n is some sort of input size). This does not give you absolute numbers or take real world factors such as cache friendliness into account. It's entirely possible that an algorithm with worse scaling actually does better on real world input in a certain size range.
-
@RememberMe -> in a certain size range.
Big-Oh isn't a practical performancse metric, it's the resilience of performance metrics to variety in input size. It's a component of reliability under unexpected circumstances, not performance for any given input size. -
@lbfalvy I never claim otherwise. I literally say that it does not give you absolute numbers, just scaling behaviour.
Perhaps this is the ambiguity: I mean "does better" = "better real world performance".
And "reliability under unexpected circumstances" is not an incorrect interpretation but I can't say I'm very fond of it. It's only really applicable when you're looking at eg. throwing a library routine at something it wasn't designed for or extreme-case analysis. -
I'll try to summarize with an example
so, assume the cost of the algorithm is 2n² + 3n
3n is not really relevant to study scalability because n² grows much faster than n
you're left with 2n², and again, the constant is not really relevant to study scalability, so you ignore that too
for all purposes, that algorithm grows at a n² pace. that's why you use the big O notation -
 Avyy7274yThis equation tells 2 things - The constant terms and the smaller degree monomials don't really change the rate of growth, so they are useless. Big O complexity is for asymptotic comparision, ie, very large n. For small n, it may be possible that a worse algo will win. For eg, an insertion sort on 5 elements will be faster than say, a radix sort. Even though radix sort is O(n).
Avyy7274yThis equation tells 2 things - The constant terms and the smaller degree monomials don't really change the rate of growth, so they are useless. Big O complexity is for asymptotic comparision, ie, very large n. For small n, it may be possible that a worse algo will win. For eg, an insertion sort on 5 elements will be faster than say, a radix sort. Even though radix sort is O(n).
Tldr, O(10000000*n) is faster than O(0.00000001*n^2) asymptotically. (There is some n0 after which linear is always better) -
 Avyy7274yRed is linear and blue is quadratic. Although red is very large at the start, blue will still win after n0=10^15
Avyy7274yRed is linear and blue is quadratic. Although red is very large at the start, blue will still win after n0=10^15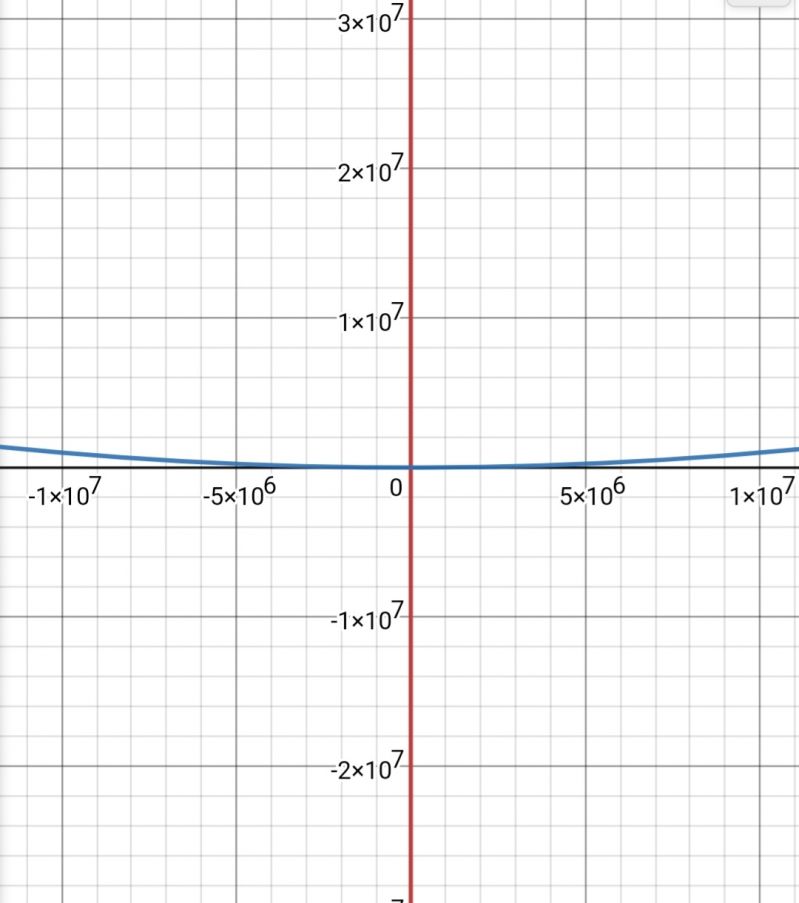
Related Rants

 This is just sad
This is just sad Algorithm strikes again! 😁
Algorithm strikes again! 😁 :)) finally a good answer
:)) finally a good answer
"f(n) is O(g(n)) if c and n0 f(n) <= cg(n) for all n > n0".
I have a couple of questions related to this equation.
1: why we use this equation?
2: which thing cg(n) is represented for?
3: what is the real-life example of this?
question
algorithm
computer science