Join devRant
Do all the things like
++ or -- rants, post your own rants, comment on others' rants and build your customized dev avatar
Sign Up
Pipeless API

From the creators of devRant, Pipeless lets you power real-time personalized recommendations and activity feeds using a simple API
Learn More
Related Rants

 So, my wife sends me this picture because our car had 111,111 miles on it. Of course she called me a nerd when...
So, my wife sends me this picture because our car had 111,111 miles on it. Of course she called me a nerd when...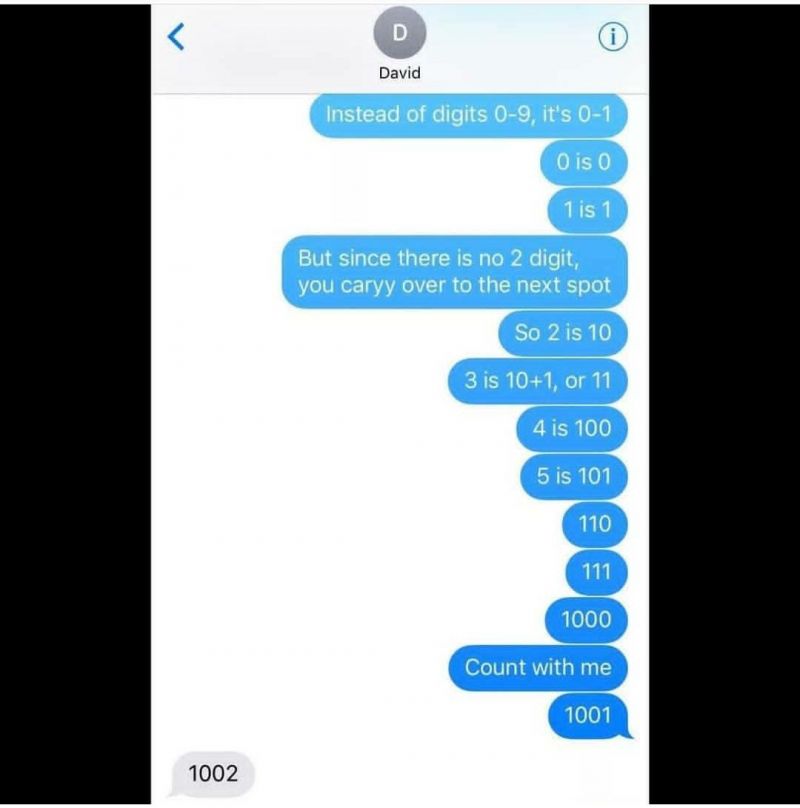 Binary is easy to teach
Binary is easy to teach EDIT: devRant April Fools joke (2018)
-------------------------
Hey everyone! As some of you have already noti...
EDIT: devRant April Fools joke (2018)
-------------------------
Hey everyone! As some of you have already noti...
What grinds my gears:
IEEE-754
This, to me, seems retarded.
Take the value 0.931 for example.
Its represented in binary as
00111111011011100101011000000100
See those last three bits? Well, it causes it to
come out in decimal like so:
0.93099999~
Which because bankers rounding is nowstandard, that actually works out to 0.930, because with bankers rounding, we round to the nearest even number? Makes sense? No. Anyone asked for it? No (well maybe the banks). Was it even necessary? Fuck no. But did we get it anyway?
Yes.
And worse, thats not even the most accurate way to represent
our value of 0.931 owing to how fucked up rounding now is becaue everything has to be pure shit these days.
A better representation would be
00111101101111101010101100110111 <- good
00111111011011100101011000000100 < - shit
The new representation works out to
0.093100004
or 0.093100003898143768310546875 when represented internally.
Whats this mean? Because of rounding you don't lose accuracy anymore.
Am I mistaken, or is IEEE-754 shit?
rant
ieee
ieee-754
binary
floating point