Taken partly from an article I just read.

Russels paradox is a problem discovered by Bertrand Russel in 1901 when studying set theory.

He describes a set that contains all sets which do not contain themselves. The set of all pornstars does not contain itself for example, so it can be include in Russel's set, as well as many others.

But what about Russel's set itself? It doesnt contain itself so shouldnt it be included as well? But that would mean it DOES include itself which means it DOESNT belong to the set. And it would keep switching like this, monotonically, forever. Hence the paradox.

If it is monotonic then where we begin in the sequence doesnt matter. So lets do away with that bugbear.

Now if russels set IS the set of all sets that dont contain themselves then we get a paradox.

However if russels set merely *has* as a single subset, all sets that dont contain themselves, then shouldnt russel's set with one level of indirection, contain itself?

In fact shouldnt all sets that DO contain themselves be a subset of sets that DONT, when taken to a sufficient nesting level?

So russels set would be a subset of sets that contain themselves, taken to 1 level of nesting, and so on..

That's some wise crack right there

Bending the spoon is impossible. You have to understand the inner truth, there is no spoon.

So it's a language paradox, not a logical paradox.
solved.

Spotted a Wisecrack from a mile ago ;)

Whut
In your formulation, Russell's set contains, as an element, a set that is the set of all sets that don't contain themselves. That's just Russell's paradox again. The enclosed set is impossible to construct since it both can and cannot contain itself. If you accept that impossibility, you can draw any conclusion you want from it, which is clearly inconsistent.

@Root logic is defined by the language you use to express it. If you want the more mathematical version:

If we let φ(x) stand for x ∈ x and let R = {x: ~φ(x)}, then R is the set whose members are exactly those objects that are not members of themselves. Contradiction.

It *is* a logical paradox tied to the ability to use any old property to define membership of a set (unrestricted set comprehension).

Isn't this problem "solved" by Gödel's theorem? There will always be paradoxes in any logical system that contains arithmetics...

@RememberMe

"thats just russels paradox again".

the game was rigged from the start.

@Ranchonyx I swear not doing it intentionally. But you have a fast eye!

@RememberMe very good response. you should be teaching. so to clarify, regardless of nesting, the members of a subset are always direct members of the outermost set (given a series of sets that are nested)?

@Wisecrack if what you're asking is
Given some objects i, j, k, l, etc. if you have sets
A = {i, j}
B = {A, k, l}
are i and j members of B?
No, they're not, at least not in the sense of the "∈" used above. Sets on their own don't "understand" what their subsets contain.

Is there some way to make B understand that it does hold i and j somewhere inside itself? Yup, define an isomorphism (essentially a function that when given B, translates it into another set C that does have the properties you want, but in a way that you can always reverse the translation to get B back from C. The ability to reverse it is a crucial property).

As a really heavy handed example imagine a "flattened" set C = {i, j, k, l}, which contains all (possibly) nested objects directly.

Imagine a function f that when given B spits out C, basically removing the nesting. So C = f(B). And the reverse is a function f' that takes C and gives back B. So B = f'(C).

Now you can define a custom "is a member" operator of your own, say "€" to mean "is a member under the isomorphism f", that is, you check membership after using f to translate the target set you're checking against. Equivalently,
x € S = x ∈ f(S)
(x is a custom-defined member of S iff it is a member of f(S), for some set S and object x)

Now with all that you can say
i € B
j € B
because what that actually says is i, j ∈ f(B) so i, j ∈ C (which is true because C does contain i and j)
because the € operator handles the translation of B into C before checking for membership. This is generally good enough for most proofs.

The isomorphism trick is a pretty common one, essentially provide a lossless translation into a form that you actually want and back, and work on the translated form.

(Lots of handwaving and loose terminology here, in reality you need to be very very careful that what you're defining is a true isomorphism or not, and if what it does is valid and allowed).

ah so B doesnt supervene the elements of its subsets.

that doesnt really make sense to me. I would think that the elements of a subset A would also be elements of subset B.

its as if the set B[i] is a different from the set from B[i][j] which I suppose is appears true. The former produces different outputs thab the latter (what you're calling a isomorphic function or something right?)

Though if what you wrote previously is true, I dont see why russels set *couldnt* be slightly redefined to contain itself with N number of nestings or subsets.

@Wisecrack as an analogy, take the list from say Python. 1 is a member of [1], but not a member of [[1]]. The list doesn't understand nesting because it doesn't have to according to its definition as an abstract data type. We generally avoid giving something more power/structure than absolutely needed. If you wanted nested element checking you can add it yourself.

Similarly sets are basic objects. Giving them the ability to understand substructure is something you don't even need most of the time (and how would you define it anyway?) so it's usually added on as needed. I guess the confusion is from the analogy of a set being a bag of items. If a bag contains another bag that contains an item, then "obviously" the outermost bag contains that item, right? Yes for irl bags, no for sets, because the ability to understand substructure is not something a set has by default. Set theory guarantees *only* direct membership.

There are many many ways to resolve the Russel Paradox by changing some stuff. The *point* of the paradox though is to show that naive set comprehension (that is, the ability to build sets any way you like) in a naive set theory (sets are just generic unordered containers which don't know anything about their elements) leads to a problem, so that theory is inconsistent and you need to be super careful while using it. Redefining it doesn't really serve any purpose because the point of the original definition was to poke a hole in set theory and redefining it doesn't make the original definition go away.

(I don't mean that it's not an interesting or useful thought experiment, just that it doesn't add to why Russel put forth that paradox)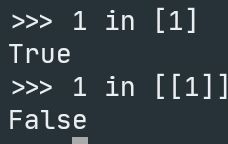

@RememberMe see this is what I meant wheb I wrote that you should be a teacher. You have a fantastic ability to communicate!

@Wisecrack haha, thanks. It has nothing to do with me, I had great teachers.

Maybe some time in the future I might actually take up teaching, good to know at least one person thinks I'm not entirely crap at it xD