Ranter
Join devRant
Do all the things like
++ or -- rants, post your own rants, comment on others' rants and build your customized dev avatar
Sign Up
Pipeless API

From the creators of devRant, Pipeless lets you power real-time personalized recommendations and activity feeds using a simple API
Learn More
Comments
-
Crop. Your. Fucking. Images.
Anyway Minecraft's world's aren't infinite, the engine begins to break after the, I believe, 32bit integer limit. -
 olback106465y@Ranchu something like that yes.
olback106465y@Ranchu something like that yes.
Wouldn't you get back to the same place if you just kept going though? The integers that store your position would overflow at some point. This means that Minecraft worlds are not infinite. They simply wrap arround. 🤔 -
@olback I wouldn't think so. The world's would be practically infinite, just the played position would be wrapped.
Should the technical limitations be considered though? If not, then there will be an exact replica I think. Kinda like the library of Babel https://libraryofbabel.info/ -
That's not how infinity works, just because it's infinite doesn't mean that there's everything in it, common misconception
-
@j4cobgarby infinite nothing is the simplest example I think.
im not familiar with infinities or sets.
is the empty set countable? -
 hitko29955y@j4cobgarby That's true for general infinity. In a special case, when you have a fixed set of possible values (e.g. digits from 0 to 9) and an infinite sequence of randomly selected values from that set (e.g. an irrational number), that sequence will contain every possible combination of values from the source set.
hitko29955y@j4cobgarby That's true for general infinity. In a special case, when you have a fixed set of possible values (e.g. digits from 0 to 9) and an infinite sequence of randomly selected values from that set (e.g. an irrational number), that sequence will contain every possible combination of values from the source set.
Each chunk in Minecraft contains 16*16*256 blocks of 133 possible kinds, so there's theoretically 6*10^52195 possible chunks, however that number is somewhat lower due to constraints imposed by Minecraft terrain generator (like no floating blocks, biomes, etc.)
The chance of having two identical chunks generated for different seeds (assuming each possible chunk is equally likely to be generated) is therefore lower than the chance of a carbon atom from the food I ate today somehow ending up on the opposite side of the universe at the exact moment the Sun blows up. However, given infinite number of Minecraft worlds it would definitely happen. -
@Ranchu Ackchyually they are exactly 60 million blocks across and at least on Java Edition there are no issues with integer limits, I believe Bedrock Edition still has issues though
-
@Ranchu Not when not modding the game or messing with the files, at least I think so.
-
@ManicRobot-- depends on the version I believe.
The first time those issues popped up was on the Java platform. -
@ManicRobot-- There are issues. When you're using floats near the 32 bit integer limit, even perlin noise starts to break.
-
@Wisecrack Nope, empty set dosent have any elements so it isnt countable. The simplest infinity is the normal number set, it is infinite but it dosent have everything in it. The true infinity in my honest opinion would be a set of transcendial numbers (those that we cant even imagine if i remember correctly) but since nobody have ever come with any examples... just take irrational numbers as a universe (everything) because there is no going back if you start thinking othervise... oh my god the i have seen the patterns in the void, they are scary. Dont go there, sane people SHOULDNT DO HARDCORE MATH. IT IS THE WORLD OF ELDRICH ABOMINATIONS and self entilted old prof pricks.
-
@Gregozor2121 ill fetch my giant abacus and infinite rock collection to see if you're correct.
give me a few minutes... -
@Gregozor2121 you mean, infinities in which you can assign a unique natural number to each element (eg. integers, natural numbers themselves) versus ones in which you can't (infinite power sets, real numbers). The first is countable.
They're both "truly" infinite though, just with slightly different properties. -
@Wisecrack Ok so given the set of rock of the size alyph 0 infinity how log would it take for the wisecrack to count the whole set given:
-counting takes 1 time unit per rock?
-counting slows down, speeds up by
a) natural number of time units?
b) times rational number?
c) statisticaly when he can take a break each time doubling time required to count with 50% propability?
-if the time required to count a rock can be any function dependent on the time elapsed from the begining of the mind experiment F?
Please write an 400x+54y page essay with pretty pictures and graphs, deadline is the 4-6i before pi will be equal to 4.22. -
@RememberMe
Yep only some infinites are countable but they dont contain "everything", in the human sense true infinity should contain it all so only uncountable can be one. Uncountable infinites have more elements than countable ones (if im not mistaken) or maybe they are both infinite? Sorry i dont have brainpower left for today.
Related Rants
-
 micheltombroff36
micheltombroff36 Another programming job: the first 5,183 decimals of pi, in wood sticks. Took me three months to do. Now I sta...
Another programming job: the first 5,183 decimals of pi, in wood sticks. Took me three months to do. Now I sta... -
 CozyPlanes15Client : Can you make some adblock? Me : Why? There is a lot of good things already... C : I mean... Listen ca...
CozyPlanes15Client : Can you make some adblock? Me : Why? There is a lot of good things already... C : I mean... Listen ca... -
 Gregozor212133
Gregozor212133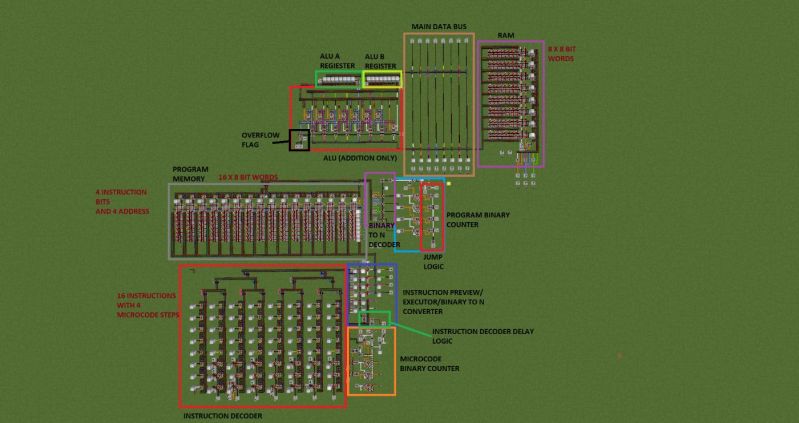 There is. My latest creation. A 8bit microcontroler made in minecraft.
Features:
(1.0 version without control ...
There is. My latest creation. A 8bit microcontroler made in minecraft.
Features:
(1.0 version without control ...

So I came across this meme and it got me thinking.
We say that if our universe is truly infinite, we are bound to find a place that is the exact replica of our local cosmic neighborhood eventually if we keep looking.
But procedurally generated worlds like minecraft have that determinism to their world structure(with an initial seed to calculate everything) where you can predict how the local neighborhood would look like at any distance, no matter how far.
So would it be correct to say that it's not guarenteed that in a game like minecraft where the world is generated procedurally with a deterministic algorithm, will be such that you can find the exact same local neighborhood from one seed in any other seed?
rant
procedural generation
infinite
minecraft