Ranter
Join devRant
Do all the things like
++ or -- rants, post your own rants, comment on others' rants and build your customized dev avatar
Sign Up
Pipeless API

From the creators of devRant, Pipeless lets you power real-time personalized recommendations and activity feeds using a simple API
Learn More
Comments
-
 jobylie66288y@mohsen yes I wanted to go on about that but I got stuck as well, so I deleted my captain obvious comment.
jobylie66288y@mohsen yes I wanted to go on about that but I got stuck as well, so I deleted my captain obvious comment. -
 jobylie66288yYou can calculate the yellow one and then thr orange one is the same. Not sure how that helps though
jobylie66288yYou can calculate the yellow one and then thr orange one is the same. Not sure how that helps though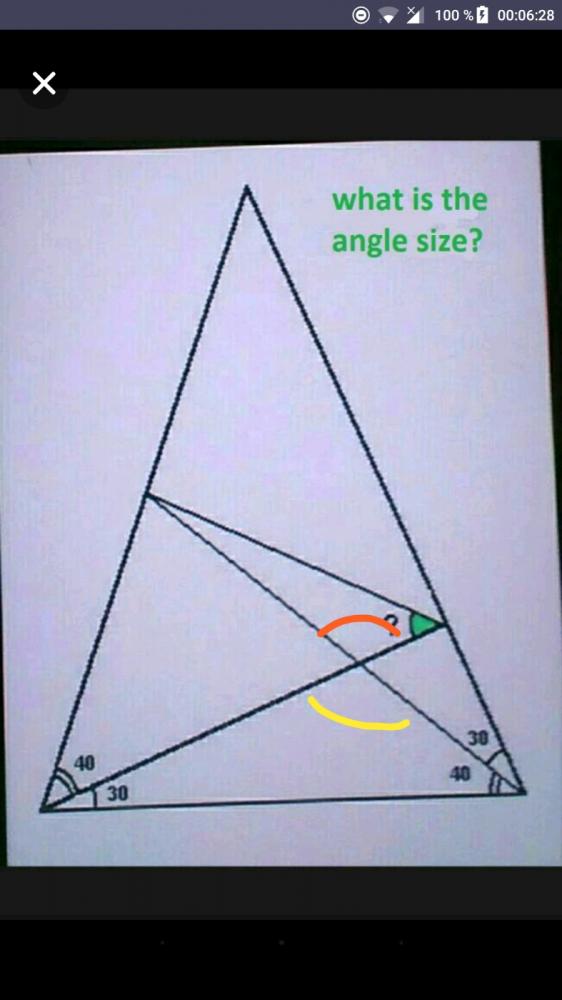
-
 Pontvs1288y@mohsen well it's 1am here and I'm tired. So here is how I know you do it. First, find all the triangles. Then use the angles you know and subtract from the total 180 in each triangle.
Pontvs1288y@mohsen well it's 1am here and I'm tired. So here is how I know you do it. First, find all the triangles. Then use the angles you know and subtract from the total 180 in each triangle. -
Damn boi, the struggle is real. I think @theScientist is wrong but I can't prove it
-
@theScientist with 50 too, and I built the figure with a software and got 50 as a solution
-
@theScientist maybe it's a joke, maybe we are just living in the matrix and this is a bug
-
Well, I have an equation like :
AEB+BEC+EBD+ABE=210
So I bet any combination works ? @tankbob seems to know what's happening. -
@theScientist Nevermind, I am stupid. I found these 4 equations :
AEB + bec = 100
ebd + bec = 70
abe + aeb = 140
abe + ebd = 110
So, according to the second one, bec needs to be in [1;70[. -
tankbob118y@theScientist you can find all but 4 angles using the triangle angles =180 rule. The bottom angle of the center triangle is 110. Therefore the desired angle is 180 - (110 + the other angle). This gives you the range of 0 to 70. I said non inclusive because you wouldn't have an angle of 0. Once you pick a value the rest of the angles can be calculated. You would need to assume the drawing is to scale and then either use a protractor or a ruler and heavy trigonometry to get a precise answer
-
I found the answer to be 40 degrees.
After getting all the angles using basic geometry. I ended up with 4 equations which can't be solved directly.
The solutions lies in the range of 0 to 70 degrees. Substitution using just whole numbers gave me the first solution to be 40 degrees. But there may be many more I guess -
 PacRat39178yi got you my friend
PacRat39178yi got you my friend
had to guess a little at the end, but making that angle 40° makes everything else make sense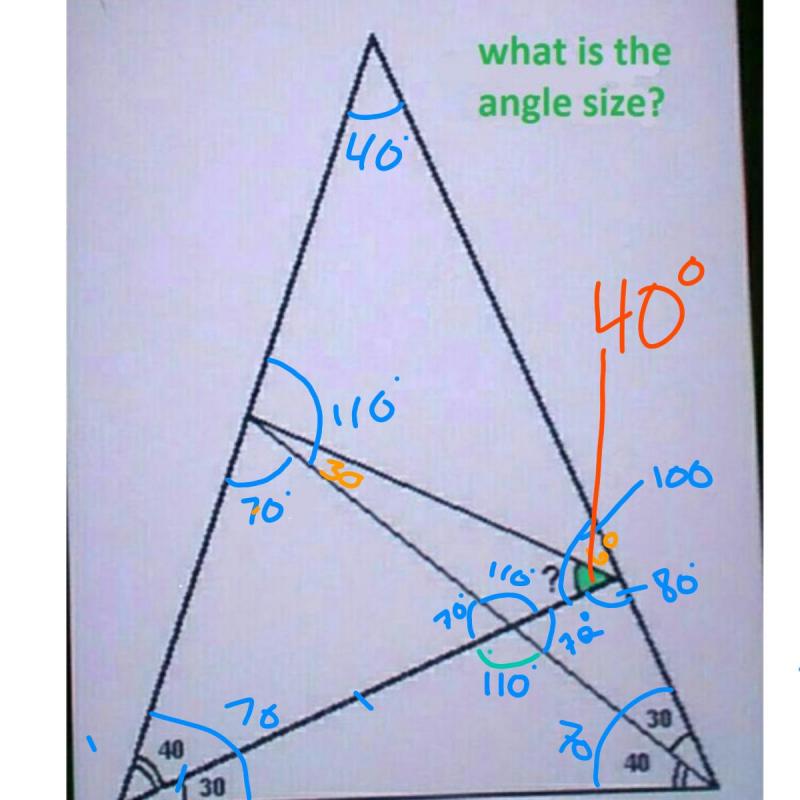
-
 mohsen878y@theScientist
mohsen878y@theScientist
Dear friend I'm so happy for your contributing. But this is a geometric problem, not algebraic! I know in geometry, every problem only have one answer. Not less, not more. Suppose it in the real world. Can a real thing has multi size? -
Stanford08yThis is an isoceles triangle. I think we may be able to use relative size to get an exact answer?
-
 mohsen878y@SupressWarnings
mohsen878y@SupressWarnings
No my friend. I saw it at a telegram channel and it's making me crazy!😂 -
40 seems to be correct. The funny thing is: I looked at it, and somehow it was the the first thing i thought of "This must be 40"
-
 mohsen878y@theScientist
mohsen878y@theScientist
You believe every answer between 0 and 70 is correct. But I show you one counterexample.
If we suppose the answer 30 is correct, so AEB = 70 and ABE = 70. Therefore ABEA is an equal legs triangle and AE = AB!
Finally we conclude that BE and CD are parallel; whereas if we extend them they cut each other!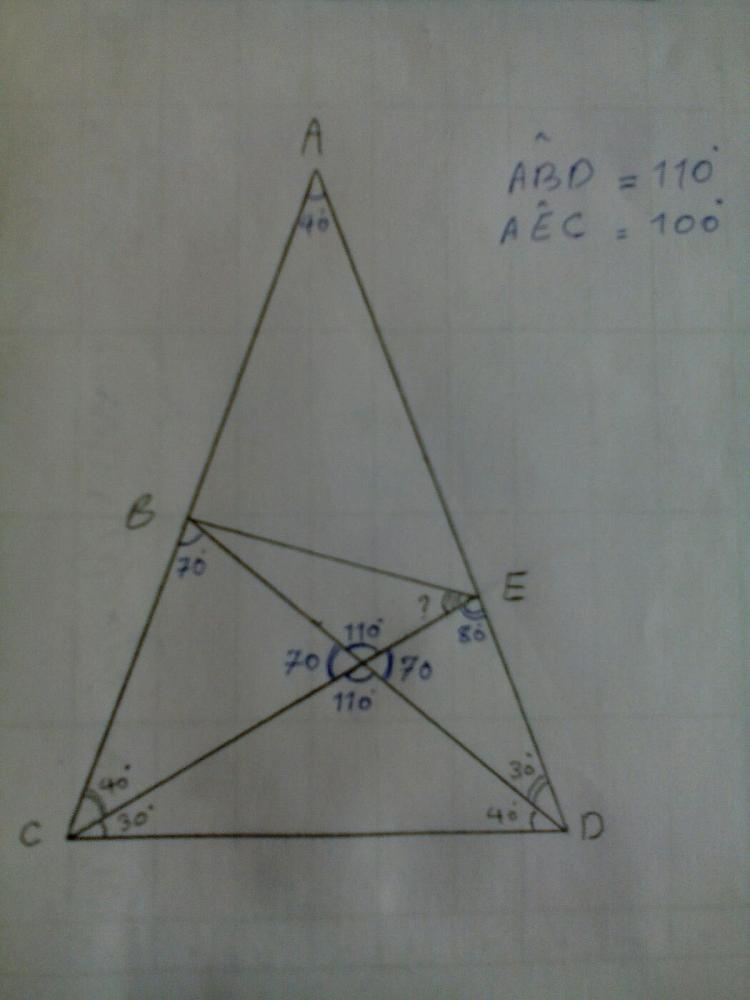
-
 PRein11708yI loved that stuff in school.
PRein11708yI loved that stuff in school.
There is a bunch you can do with trigonometry to get relative sizes of sides but I got stuck at some point.
The similar triangles help too.
And ffs not every answer works. If we had less info on the image, maybe. But in this case it's pretty specific. -
 donuts232418yThis the is an interesting discussion... Perhaps we should make a Collaborate to solve it 😁
donuts232418yThis the is an interesting discussion... Perhaps we should make a Collaborate to solve it 😁 -
 PRein11708y@theScientist an answer of 30 for example would lead to the upper most triangle to have 40 70 70 angles making his sides equal which they obviously aren't.
PRein11708y@theScientist an answer of 30 for example would lead to the upper most triangle to have 40 70 70 angles making his sides equal which they obviously aren't.
You are basing the "anything works" answer on an equation that doesn't describe the figure fully. -
This problem is referred to as the "world's hardest easy geometry problem", so you can find the solution. (I don't have the time to do it right now, so maybe I will post about it later)
-
tankbob118y@PRein When these kind of questions are set in an exam you are supposed to assume that the diagram is not to scale and only rely on the figures. Hence 0 to 70 non inclusive being a mathematically correct answer.
-
tankbob118yOf course the answer could be 30 because the other 30 degree angles are marked with a single curve whilst the 40s are marked with a double arc
-
 pajaja17218yWhat he probably wanted to say is that if you do build this with walls you could build infinite number of walls that make 0-70 angle between them and that all of them would satisfy the constraints that he extracted from problem description. I tried to solve this the other way, with trigonometry and i got a specific angle, it's just not pretty so I'm not sure it's correct.
pajaja17218yWhat he probably wanted to say is that if you do build this with walls you could build infinite number of walls that make 0-70 angle between them and that all of them would satisfy the constraints that he extracted from problem description. I tried to solve this the other way, with trigonometry and i got a specific angle, it's just not pretty so I'm not sure it's correct. -
 pajaja17218ySure, so idea was to pick two triangles that have one common side and a second side of equal length (will be apparent why later) and use a law of sines to make two equations. ( http://mathworld.wolfram.com/LawofS... )
pajaja17218ySure, so idea was to pick two triangles that have one common side and a second side of equal length (will be apparent why later) and use a law of sines to make two equations. ( http://mathworld.wolfram.com/LawofS... )
Also since we know that sum of those two angles is 70, and the other one (labeled Y) was easier to calculate I picked it.
So using law of sines i got first two equations and expressed side DC via them. Since ECB is isosceles sides BC and EC are equal, so we can eliminate them from the equation.
-
 pajaja17218yPart 2: Since I haven't done trigonometry in like 5+ years i used this guy to solve Y (theta) for me and subtracted it from 70 to get X.
pajaja17218yPart 2: Since I haven't done trigonometry in like 5+ years i used this guy to solve Y (theta) for me and subtracted it from 70 to get X.
-
@theScientist oops, first page of chapter 12. I meant p 39 of the PDF, but it's p. 33
-
jamestha3d38yGuys. i think this problem can only be solved using trigonometry. in the similar problems posted by @garrheauarthur, there was a fundamental equilateral triangle emerging which solved enabled solving it with geometry, for this one i do not think so.
-
jamestha3d38yThis is what I got, solved by hand. I really doubt geometry wil l give us the answer to this one

-
tankbob118y@jamestha3d Well done. I got so caught up in the fact there wasn't enough information to solve it that I didn't twig that we had the isoceles to give us the required sides.
-
jamestha3d38y@industry-monkey <EAB = 30, <ABE = 70. These were given. So <AEB = 180 -30 -70 = 80.
-
jamestha3d38y@theScientist I've seen the link you sent, but there's a fundamental difference between that question and this one. First of all, the angle, which we are looking for, subtends lower in this particular problem. And secondly, the other problem was solvable by geometry because the respective angles make it easy to obtain an equilateral triangle which is key to solving that equation. I will post my attempted geometrical solution, I got stuck after I found that the angle was 30 + α and couldn't get the value of α.
-
 mohsen878yWell my friends,,,
mohsen878yWell my friends,,,
I calculate that by 123D design. As you see the answer is 45.7 . So the @pajaja and @jamestha3d final answers are exactly correct!
Thank you all my friends.😉 Good luck...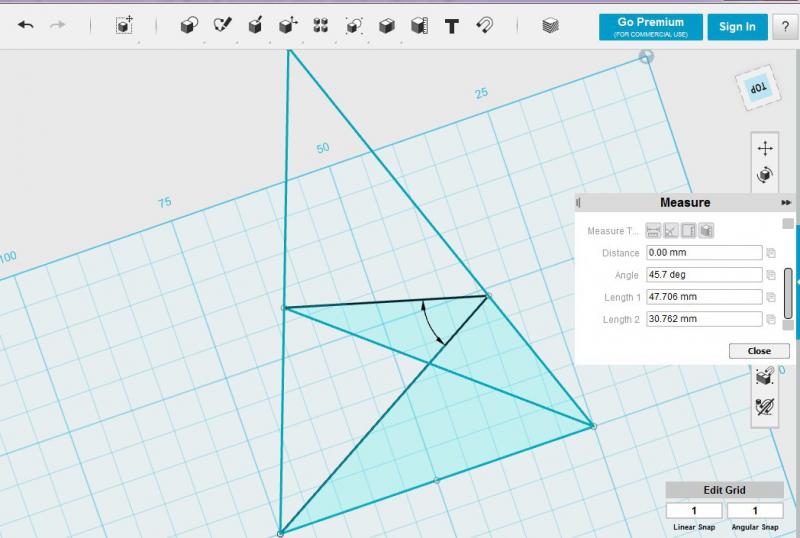
-
jamestha3d38y@mohsen nice. Well done. I think this proves there is no geometric solution? Because how do you get .7 degrees in geometry? Best I could get was to prove that the angle was between 30 and 70 degrees.
-
 pajaja17218yWhy would this prove there's no geometric solution? I provided one, you did too. Also why wouldn't you have .7 degrees? If you don't like writing decimal points, every degree has 60 minutes, every minute has 60 seconds so you can use those.
pajaja17218yWhy would this prove there's no geometric solution? I provided one, you did too. Also why wouldn't you have .7 degrees? If you don't like writing decimal points, every degree has 60 minutes, every minute has 60 seconds so you can use those. -
jamestha3d38y@pajaja no. You provided a trigonometric solution. Using sines of angle. A geometric solution would only use constructing extra lines and Euclidean theorems. Something like the ones in the link @garrheauarthur posted. I'll brb with an example
-
jamestha3d38y@pajaja here's what I mean. I tried adding other lines, and doing other deductions didn't get much farther than this. And if the angle of 45.7 degrees is right, I do not think there is anyway you can get an answer like this using plain geometry. Some other versions of this question (using different values of angles) can be solved like that though.

Related Rants



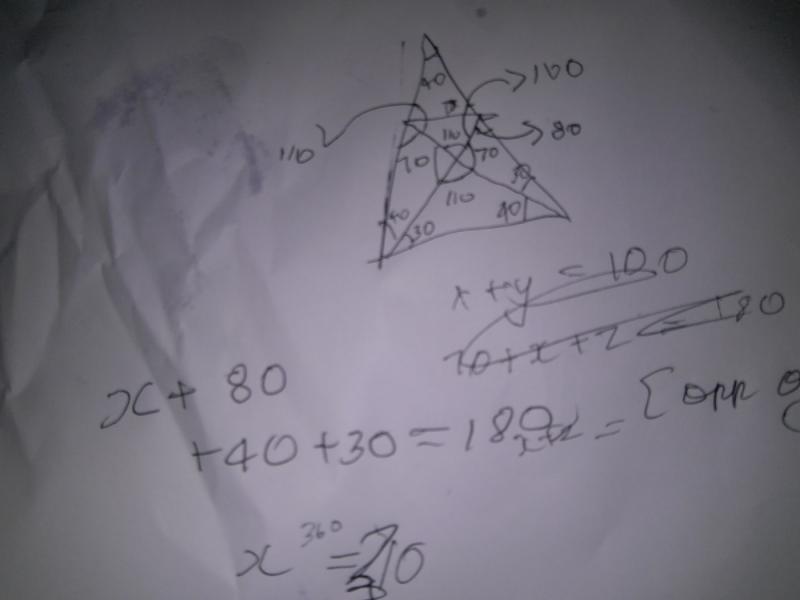
 Going to try this...LOL 😂😂
Going to try this...LOL 😂😂 I am Computer Science Student
Yesterday I asked question to my classmates, what is Linux,
here's some(non-fo...
I am Computer Science Student
Yesterday I asked question to my classmates, what is Linux,
here's some(non-fo... A possibile interview answer
A possibile interview answer
Please help me to find it.🙏
undefined
question
sharp
angle
degree
smart