Ranter
Join devRant
Do all the things like
++ or -- rants, post your own rants, comment on others' rants and build your customized dev avatar
Sign Up
Pipeless API

From the creators of devRant, Pipeless lets you power real-time personalized recommendations and activity feeds using a simple API
Learn More
Comments
-
 Root772337yMultiplication before division
Root772337yMultiplication before division
Following PEMDAS in order without "grouping" them avoids ambiguity.
() ^ × ÷ + - -
And that's why we have (reverse) polish notation which are completely unambiguous.
-
@Codex404 I'm not even sure I can write it correctly and I wish I could but infix is such an international "standard" that it won't be easy to change it...
-
@Marowski infix is more readable for humans IMO but can be ambiguous also every calculator has to transform what you write into an "executable" or "interpretable" format which resembles the (reverse) polish notation as it usually execute operations as one stack of operands, and one of operators.
-
9 is correct but 1 is not wrong either. This is not math anymore, it is just some tricks based on personal opinions.
Math needs to be absolute, pure and only based on logic. The order stuff is bullshit as whole. Parenthesis are our ally.
The one who writes such equations needs to specify what operation to do first by further parenthesis, since their operation order is the same. Gosh i hate these kind of tricks. -
@davenall no. You can't exactly say why multiplication comes before division or vice versa. It needs parenthesis.
-
@davenall No it didn't explain anything and it can work like that. You don't pull 0.33 from thin air, it is already there.
6 ÷ ( 2 * ( 1+2 ) ) = 1 - not correct, not wrong either. Can be perceived like this.
( 6 ÷ 2 ) * ( 1 + 2 ) = 9 - acccepted based on PEMDA.
According to PEMDA, 9 is correct. I didnt say 1 is correct either, you are like defending yourself as i said 1 is correct. What i just say is that needs specification and these whole thing is bullcrap and not maths. -
@davenall I am not changing the problem. I am just showing two possibilities and showing you how parenthesis gets rid of this stupidity.
We circled back to where we started. By what standarts ? By which proof ? By what implication can you say it is not correct ? If this would be a definite and absolute, i wouldn't be able to tweak it without breaking the rules. But as you see, i can. Both solution is not completely wrong.
Jeez, forget about it. This is going nowhere, i wish you happiness inside of relativeness and confusion on math, while having to rely on your previous knowledge.
Math should be timeless, so that even someone who doesn't know anything about these can't get into confusion, exactly like this. -
 taglia5667yYou are all wrong.
taglia5667yYou are all wrong.
The answer isn't 9.
The answer isn't 1 either.
.. The answer is 42. -
Everybody has made up their mind that the method they learned in school is right. There should've been a single standard like iupac for chemistry
-
@ausername thee is a single standard as far as I know, the issue is that it changed 3 times since 1900..
-
Please Excuse My Dear Aunt Sally
Multiplication and division are done in order left to right.
Then addition and subtraction are done in order left to right.
The answer is 9.
One thing you can say about math is it’s the most consistent thing on the planet. If you get a different answer, you’re doing it wrong. -
 devios156307yI hate arguing about this but I have a math degree and the answer is 1.
devios156307yI hate arguing about this but I have a math degree and the answer is 1.
The real reason is that implicit multiplication creates a term and terms cannot be split across a division line.
Mathematicians never use the × or ÷ symbols because of their ambiguities. BEDMAS/PEMDAS are things taught in grade school and are not relevant in higher mathematics because the notation is different and unambiguous.
Personally I don’t even think they should teach that notation because of how confusing it is and how much clearer real algebraic notation is. Just look at how many people fight about it. -
 devios156307yThe real answer is it's ambiguous, because you're combining two different and incompatible notations. But 1 is the correct answer if you follow algebraic notation, from which implicit multiplication comes.
devios156307yThe real answer is it's ambiguous, because you're combining two different and incompatible notations. But 1 is the correct answer if you follow algebraic notation, from which implicit multiplication comes.
And like I said if by divide you mean a line of division, then certainly the implicitly multiplied term would be below the line of division. -
 devios156307yIn short, the image is how you would write it in correct algebraic notation.
devios156307yIn short, the image is how you would write it in correct algebraic notation.
In grade school notation you need to use an explicit × to make it clear:
6 ÷ 2 × (2 + 1) = 9
6÷2(2+1) is invalid as it combines two incompatible notations.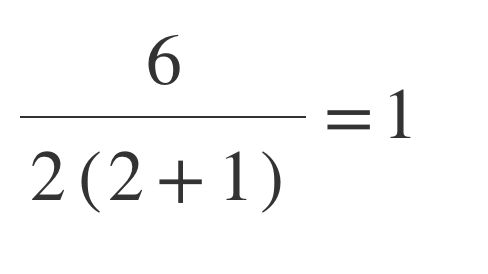
-
 devios156307y@davenall The point is 6÷2(2+1) is ambiguous, so either answer you cite is arguably correct depending on how you interpret it. But that's entirely the problem. It's an invalid notation *because* it's ambiguous and I would therefore rather argue that it has no answer.
devios156307y@davenall The point is 6÷2(2+1) is ambiguous, so either answer you cite is arguably correct depending on how you interpret it. But that's entirely the problem. It's an invalid notation *because* it's ambiguous and I would therefore rather argue that it has no answer. -
 devios156307yAnd just to cover my ass in case anyone calls me out on it, you actually *can* split a term across a line of division with negative exponentiation, but the term is still treated as a singular entity with higher precedence than adjacent operators.
devios156307yAnd just to cover my ass in case anyone calls me out on it, you actually *can* split a term across a line of division with negative exponentiation, but the term is still treated as a singular entity with higher precedence than adjacent operators. -
 devios156307y@davenall I’m sorry but you and all of those sources are wrong. You cannot split an implicitly multiplied term across a line of division without negative exponentiation. The 2(2+1) has to be treated as a singular term. Either the whole thing is above a line of division or below one.
devios156307y@davenall I’m sorry but you and all of those sources are wrong. You cannot split an implicitly multiplied term across a line of division without negative exponentiation. The 2(2+1) has to be treated as a singular term. Either the whole thing is above a line of division or below one.
That’s what my bachelors in Mathematics tells me.
So whatever the answer is, it’s *not* 9. It’s either 1 or it’s undefined. I’m fine with either. -
 devios156307y@davenall I can give you a really simple example to clear this up.
devios156307y@davenall I can give you a really simple example to clear this up.
Suppose we had the formula 6/2a. It’s easier to picture 2a as a term when you have variables.
Now sub in 2+1 as the value of a:
6/2(2+1)
We can’t suddenly start treating what used to be a single term (2a) as two different terms. -
 devios156307yHere are the two ambiguous interpretations written properly in (unambiguous) algebraic notation. I've put boxes around all of the terms at the various levels so you can see that a) 2(2+1) is itself an entire term, and b) at no point in the interpretation that gives you the answer of 9 do you see the term 2(2+1).
devios156307yHere are the two ambiguous interpretations written properly in (unambiguous) algebraic notation. I've put boxes around all of the terms at the various levels so you can see that a) 2(2+1) is itself an entire term, and b) at no point in the interpretation that gives you the answer of 9 do you see the term 2(2+1).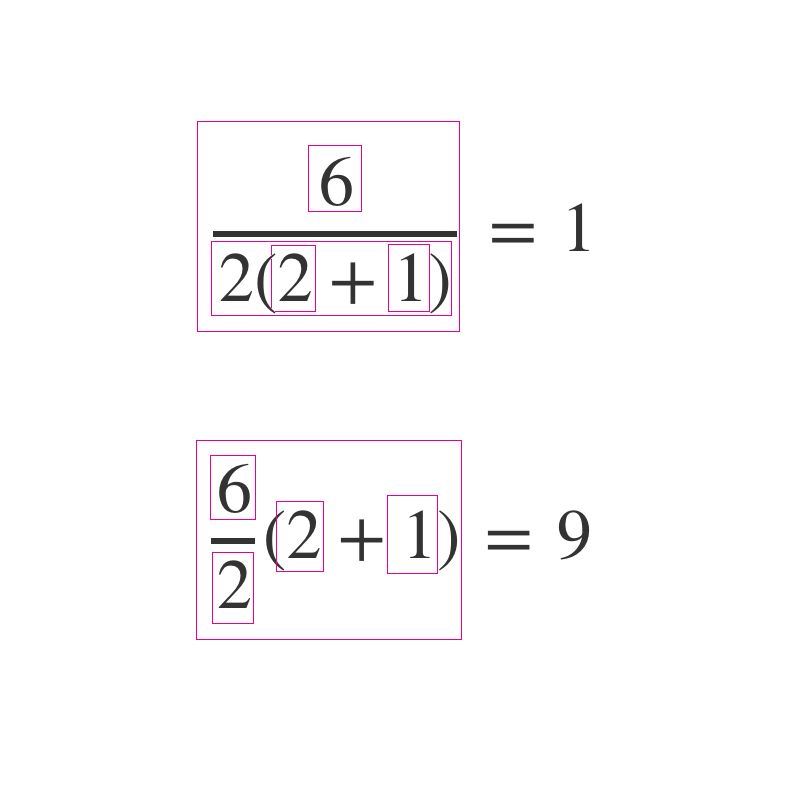
-
 devios156307y@davenall I completely agree that carrying the convention back to arithmetic is problematic. Indeed it's the heart of the problem.
devios156307y@davenall I completely agree that carrying the convention back to arithmetic is problematic. Indeed it's the heart of the problem.
But I stand firm that if you're going to write something as a term, you need to respect the definition of what a term is, even if you're bringing that back to arithmetic notation, but I still say it should never be done in the first place.
Perhaps we can at least agree on that. :) -
 devios156307y@davenall Also in algebra 23 can never mean 2 * 3. That's not a valid interpretation. If you want to include two reals in the same term you can use the ∙ operator, as in 2∙3 or you can write it as 2(3).
devios156307y@davenall Also in algebra 23 can never mean 2 * 3. That's not a valid interpretation. If you want to include two reals in the same term you can use the ∙ operator, as in 2∙3 or you can write it as 2(3). -
 devios156307y@davenall Thanks for being level-headed about it. Trust me I understand where you're coming from, but as you can see my education gives me reason to disagree with those interpretations.
devios156307y@davenall Thanks for being level-headed about it. Trust me I understand where you're coming from, but as you can see my education gives me reason to disagree with those interpretations.
I'm not on Twitter or anything social besides this and Facebook really but if you want you can email me at logan at devios.one. :)
My github is at https://github.com/devios1 including a goofy (and old) picture of me, lol. -
 -vim-30837yThe equation is just wrong! It’s using algebric term notation with arithmetic ÷ notation. Now, as there’s no reason why this would be algebra, and it seams like an arithmetic equation, you need to expand to multiplication: 6 ÷ 2 × (1 + 2), which is equal to 9. Anyway, you should never cross the two notations, except maybe on calculators, to make it faster to write.
-vim-30837yThe equation is just wrong! It’s using algebric term notation with arithmetic ÷ notation. Now, as there’s no reason why this would be algebra, and it seams like an arithmetic equation, you need to expand to multiplication: 6 ÷ 2 × (1 + 2), which is equal to 9. Anyway, you should never cross the two notations, except maybe on calculators, to make it faster to write. -
 devios156307y@davenall That pretty much hits the nail on the head, although I disagree with his suggestion that algebraic notation is "historical".
devios156307y@davenall That pretty much hits the nail on the head, although I disagree with his suggestion that algebraic notation is "historical".
It is a lot harder to type on a keyboard though. 😜 -
 devios156307y@irene If you think of a term as being implicitly wrapped in parentheses I guess you could put it that way, but I think the real problem is that juxtaposition doesn't belong in arithmetic notation at all.
devios156307y@irene If you think of a term as being implicitly wrapped in parentheses I guess you could put it that way, but I think the real problem is that juxtaposition doesn't belong in arithmetic notation at all.
I also happen to disagree with PEMDAS, despite it being "the rule". So yeah. -
 devios156307y@irene I just mean I don't normally visualize it like that, but you're right it's exactly equivalent.
devios156307y@irene I just mean I don't normally visualize it like that, but you're right it's exactly equivalent. -
 devios156307y@davenall I actually just used an online LaTeX editor (www.hostmath.com) to get the formulas and drew the boxes in Photoshop. 🙂
devios156307y@davenall I actually just used an online LaTeX editor (www.hostmath.com) to get the formulas and drew the boxes in Photoshop. 🙂
Related Rants



 Boolean Logic....
Boolean Logic.... Project manager logic.
Project manager logic.
Having debates on order of operations. The one that is hot again is the 6÷2(2+1).
Programming and actual order of operations says the answer is 9, but everyone argues it is 1. Well before 1970 that was the case. SMH. Despite showing them the rules and work, they still say theirs is the correct way.
With programming and Excel formulas I deal with every day I do this without even pausing.
rant
pemdas
logic