Join devRant
Do all the things like
++ or -- rants, post your own rants, comment on others' rants and build your customized dev avatar
Sign Up
Pipeless API

From the creators of devRant, Pipeless lets you power real-time personalized recommendations and activity feeds using a simple API
Learn More
Search - "floating point numbers"
-
Try not to use floating point numbers in places where precision is important. Like for instance, money. Always store the base value where it makes the most sense
 15
15 -
Second semester
Java - OOP Course
We had to write a game, an arkanoid clone
Neat shit
And a fun course, mad respect to the Prof.
BUT
Most students, including me had this ONE bug where the ball would randomly go out of the wall boundaries for no clear reason.
A month passed, sleepless nights, no traces.
Two months later. Same shit. Grades going down (HW grades) because it became more and more common, yet impossible to track down.
3 months later, we had to submit the HW for the last time which included features like custom level sets, custom blocks and custom layouts.
So before we submit the game for review, they had pre-defined level sets that we had to include for testing sake.
I loaded that.
The bug is back.
But
REPRODUCIBLE.
OMG.
So I started setting up breakpoints.
And guess what the issue was.
FLOATING FUCKING POINT NUMBERS
(Basically the calculations were not as expected)
Changing to Ints did it's job and the bug was officially terminated.
Most satisfying night yet.
Always check your float number calculations as it's never always what you expect.
Lesson learned, use Ints whenever possible.18 -
POSTMORTEM
"4096 bit ~ 96 hours is what he said.
IDK why, but when he took the challenge, he posted that it'd take 36 hours"
As @cbsa wrote, and nitwhiz wrote "but the statement was that op's i3 did it in 11 hours. So there must be a result already, which can be verified?"
I added time because I was in the middle of a port involving ArbFloat so I could get arbitrary precision. I had a crude desmos graph doing projections on what I'd already factored in order to get an idea of how long it'd take to do larger
bit lengths
@p100sch speculated on the walked back time, and overstating the rig capabilities. Instead I spent a lot of time trying to get it 'just-so'.
Worse, because I had to resort to "Decimal" in python (and am currently experimenting with the same in Julia), both of which are immutable types, the GC was taking > 25% of the cpu time.
Performancewise, the numbers I cited in the actual thread, as of this time:
largest product factored was 32bit, 1855526741 * 2163967087, took 1116.111s in python.
Julia build used a slightly different method, & managed to factor a 27 bit number, 103147223 * 88789957 in 20.9s,
but this wasn't typical.
What surprised me was the variability. One bit length could take 100s or a couple thousand seconds even, and a product that was 1-2 bits longer could return a result in under a minute, sometimes in seconds.
This started cropping up, ironically, right after I posted the thread, whats a man to do?
So I started trying a bunch of things, some of which worked. Shameless as I am, I accepted the challenge. Things weren't perfect but it was going well enough. At that point I hadn't slept in 30~ hours so when I thought I had it I let it run and went to bed. 5 AM comes, I check the program. Still calculating, and way overshot. Fuuuuuuccc...
So here we are now and it's say to safe the worlds not gonna burn if I explain it seeing as it doesn't work, or at least only some of the time.
Others people, much smarter than me, mentioned it may be a means of finding more secure pairs, and maybe so, I'm not familiar enough to know.
For everyone that followed, commented, those who contributed, even the doubters who kept a sanity check on this without whom this would have been an even bigger embarassement, and the people with their pins and tactical dots, thanks.
So here it is.
A few assumptions first.
Assuming p = the product,
a = some prime,
b = another prime,
and r = a/b (where a is smaller than b)
w = 1/sqrt(p)
(also experimented with w = 1/sqrt(p)*2 but I kept overshooting my a very small margin)
x = a/p
y = b/p
1. for every two numbers, there is a ratio (r) that you can search for among the decimals, starting at 1.0, counting down. You can use this to find the original factors e.x. p*r=n, p/n=m (assuming the product has only two factors), instead of having to do a sieve.
2. You don't need the first number you find to be the precise value of a factor (we're doing floating point math), a large subset of decimal values for the value of a or b will naturally 'fall' into the value of a (or b) + some fractional number, which is lost. Some of you will object, "But if thats wrong, your result will be wrong!" but hear me out.
3. You round for the first factor 'found', and from there, you take the result and do p/a to get b. If 'a' is actually a factor of p, then mod(b, 1) == 0, and then naturally, a*b SHOULD equal p.
If not, you throw out both numbers, rinse and repeat.
Now I knew this this could be faster. Realized the finer the representation, the less important the fractional digits further right in the number were, it was just a matter of how much precision I could AFFORD to lose and still get an accurate result for r*p=a.
Fast forward, lot of experimentation, was hitting a lot of worst case time complexities, where the most significant digits had a bunch of zeroes in front of them so starting at 1.0 was a no go in many situations. Started looking and realized
I didn't NEED the ratio of a/b, I just needed the ratio of a to p.
Intuitively it made sense, but starting at 1.0 was blowing up the calculation time, and this made it so much worse.
I realized if I could start at r=1/sqrt(p) instead, and that because of certain properties, the fractional result of this, r, would ALWAYS be 1. close to one of the factors fractional value of n/p, and 2. it looked like it was guaranteed that r=1/sqrt(p) would ALWAYS be less than at least one of the primes, putting a bound on worst case.
The final result in executable pseudo code (python lol) looks something like the above variables plus
while w >= 0.0:
if (p / round(w*p)) % 1 == 0:
x = round(w*p)
y = p / round(w*p)
if x*y == p:
print("factors found!")
print(x)
print(y)
break
w = w + i
Still working but if anyone sees obvious problems I'd LOVE to hear about it.36 -
I was working on a project lately where I needed to convert an array of bits (1s and 0s) to floating numbers.
It is quite straightforward how to convert an array of bits to the simple integer (i.e. [101] = 5). But what about the numbers like `3.1415` (𝝿) or `9.109 × 10⁻³¹` (the mass of the electron in kg)?
I've explored this question a bit and came up with a diagram that explains how the float numbers are actually stored.
There is also an interactive version of this diagram available here https://trekhleb.dev/blog/2021/....
Feel free to experiment with it and play around with setting the bits on and off and see how it influences the final result.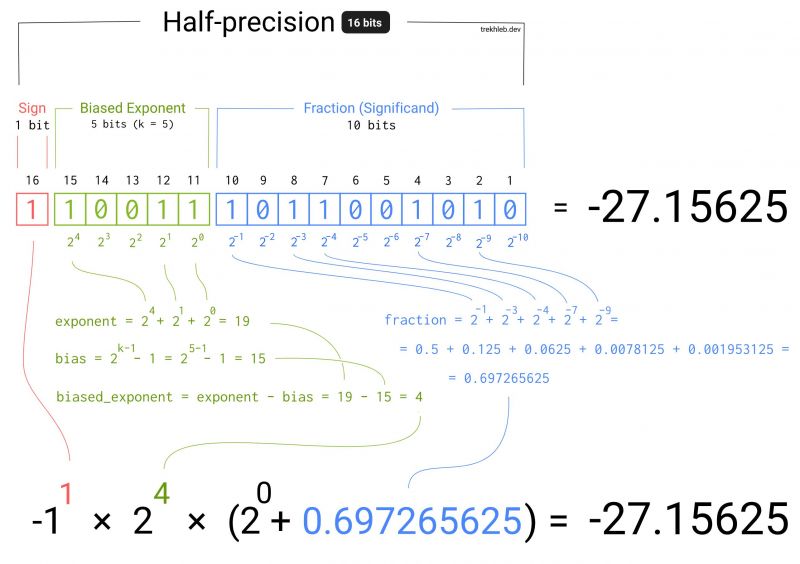 13
13 -
When you’re trying to write a function to convert a base 10 integer to a base 2 integer in Javascript without using parseInt() and it takes you a while to realize that you’re used to integer division being integer division and have forgotten that JavaScript stores numbers as double precision floating point. *facepalm*1
-
When we subtract some number m from another number n, we are essentially creating a relationship between n and m such that whatever the difference is, can be treated as a 'local identity' (relative value of '1') for n, and the base then becomes '(base n/(n-m))%1' (the floating point component).
for example, take any number, say 512
697/(697-512)
3.7675675675675677
here, 697 is a partial multiple of our new value of '1' whose actual value is the difference (697-512) 185 in base 10. proper multiples on this example number line, based on natural numbers, would be
185*1,
185*2
185*3, etc
The translation factor between these number lines becomes
0.7675675675675677
multiplying any base 10 number by this, puts it on the 1:185 integer line.
Once on a number line other than 1:10, you must multiply by the multiplicative identity of the new number line (185 in the case of 1:185), to get integers on the 1:10 integer line back out.
185*0.7675675675675677 for example gives us
185*0.7675675675675677
142.000000000000
This value, pulled from our example, would be 'zero' on the line.
185 becomes the 'multiplicative' identity of the 1:185 line. And 142 becomes the additive identity.
Incidentally the proof of this is trivial to see just by example. if 185 is the multiplicative identity of 697-512, and and 142 is the additive identity of number line 1:185
then any number '1', or k=some integer, (185*(k+0.7675675675675677))%185
should equal 142.
because on the 1:10 number line, any number n%1 == 0
We can start to think of the difference of any two integers n, as the multiplicative identity of a new number line, and the floating point component of quotient of any number n to the difference of any number n-m, as the additive identity.
let n =697
let m = 185
n-m == '1' (for the 1:185 line)
(n-m) * ((n/(n-m))%1) == '0'
As we can see just like on the integer number line, n%1 == 0
or in the case of 1:185, it equals 142, our additive identity.
And now, the purpose of this long convoluted post: all so I could bait people into reading a rant on division by zero.21 -
Floating point numbers! 😖
Writing geometric algorithms for CNC machining... you'll find those 10th decimal place inconsistencies real quick!1 -
Why the fuck is it so hard to write a simple bash script. Syntax so strange and so many symbols you need to know. If you need to do calculations with floating point numbers, the mess is perfect.10
-
ISO floating point numbers are essentially wrapped in a hardware-level monad because the normal meaningful values aren't closed over basic arithmetic so conceptually wrapping everything in Maybe using the 'infectious sentinel value' NaN leads to substantial speedups.
With this in mind, I think high-level languages that have a Maybe should use those and have the language-type float refer to a floating point that isn't NaN.2 -
I'm at uni learning about floating point numbers and IEEE 754 and its so different to what I learnt at A-Level and it seems that using twos compliment floating point numbers is more efficient than storing numbers than IEEE 754 as IEEE 754 seems to use sign and magnitude. So why do we use IEEE 754?1
-
Just working with numbers these days i wonder if i can compile gcc with fixed point support , like if i use float in source it should implement my fixed point implementation rather than ieee floating point standards6
-
floating point numbers are workarounds for infinite problems people didn’t find solution yet
if you eat a cake there is no cake, same if you grab a piece of cake, there is no 3/4 cake left there is something else yet to simplify the meaning of the world so we can communicate cause we’re all dumb fucks who can’t remember more than 20000 words we named different things as same things but in less amount, floating point numbers were a biggest step towards modern world we even don’t remember it
we use infinity everyday yet we don’t know infinite, we only partially know concept of null
you say piece of cake but piece is not measurement - piece is infinite subjective amount of something
everything that is subjective is infinite, like you say a sentence it have infinite number of meanings, you publish a photo or draw a paining there are infinite number of interpretations
you can say there is no cake but isn’t it ? you just said cake so your mind want to materialize something you already know and since you know the cake word there is a cake cause it’s infinite once created
if you think really hard and try to get that feeling, the taste of your last delicious cake you can almost feel it on your tongue cause you’re connected to every cake taste you ate
someone created cake and once people know what cake is it’s infinite in that collection, but what if no one created cake or everyone that remember how cake looks like died, everything what’s cake made of extinct ? does it exist or is it null ? that’s determinism and entropy problem we don’t understand, we don’t understand past and future cause we don’t understand infinity and null, we just replaced it with time
there is no time and you can have a couple of minutes break are best explanations of how null and infinite works in a concept of time
so if you want to change the world, find another thing that explains infinity and null and you will push our civilization forward, you don’t need to know any physics or math, you just need to observe the world and spot patterns8 -
Why do we still use floating-point numbers? Why not use fixed-point?
Floating-point has precision errors, and for some reason each language has a different level of error, despite all running on the same processor.
Fixed-point numbers don't have precision issues (unless you get way too big, but then you have another problem), and while they might be a bit slower, I don't think there is enough of a difference in speed to justify the (imho) stupid, continued use of floating-point numbers.
Did you know some (low power) processors don't have a floating-point processor? That effectively makes it pointless to use floating-point, it offers no advantage over fixed-point.
Please, use a type like Decimal, or suggest that your language of choice adds support for it, if it doesn't yet.
There's no need to suffer from floating-point accuracy issues.26
