Join devRant
Do all the things like
++ or -- rants, post your own rants, comment on others' rants and build your customized dev avatar
Sign Up
Pipeless API

From the creators of devRant, Pipeless lets you power real-time personalized recommendations and activity feeds using a simple API
Learn More
Search - "prime numbers"
-
Back in the days when I started to learn c I had an assignment to print all the prime numbers between 1 to 100 but didn't know how (with if/for/while)
So I searched Google for "prime numbers from 1 to 100" and used printf to print them on the screen
I got an A+7 -
There is NOTHING more satisfying than having an algorithm suddenly click while you are in the shower.
I got a program for determining Prime Numbers using Extended Euclid Algorithm from ~2 to .28 seconds <35 -
A few weeks ago at infosec lab in college
Me: so I wrote the RSA code but it's in python I hope that's ok (prof usually gets butthurt if he feels students know something more than him)
Prof: yeah, that's fine. Is it working?
Me: yeah, *shows him the code and then runs it* here
Prof: why is it generating such big ciphertext?
Me: because I'm using big prime numbers...?
Prof: why are you using big prime numbers? I asked you to use 11, 13 or 17
Me: but that's when we're solving and calculating this manually, over here we can supply proper prime numbers...
Prof: no this is not good, it shouldn't create such big ciphertext
Me: *what in the shitting hell?* Ok....but the plaintext is also kinda big (plaintext:"this is a msg")
Prof: still, ciphertext shows more characters!
Me: *yeah no fucking shit, this isn't some mono/poly-alphabetic algorithm* ok...but I do not control the length of the ciphertext...? I only supply the prime numbers and this is what it gives me...? Also the code is working fine, i don't think there's any issue with the code but you can check it if there are any logic errors...
Prof: *stares at the screen like it just smacked his mom's ass* fine
Me: *FML*12 -
POSTMORTEM
"4096 bit ~ 96 hours is what he said.
IDK why, but when he took the challenge, he posted that it'd take 36 hours"
As @cbsa wrote, and nitwhiz wrote "but the statement was that op's i3 did it in 11 hours. So there must be a result already, which can be verified?"
I added time because I was in the middle of a port involving ArbFloat so I could get arbitrary precision. I had a crude desmos graph doing projections on what I'd already factored in order to get an idea of how long it'd take to do larger
bit lengths
@p100sch speculated on the walked back time, and overstating the rig capabilities. Instead I spent a lot of time trying to get it 'just-so'.
Worse, because I had to resort to "Decimal" in python (and am currently experimenting with the same in Julia), both of which are immutable types, the GC was taking > 25% of the cpu time.
Performancewise, the numbers I cited in the actual thread, as of this time:
largest product factored was 32bit, 1855526741 * 2163967087, took 1116.111s in python.
Julia build used a slightly different method, & managed to factor a 27 bit number, 103147223 * 88789957 in 20.9s,
but this wasn't typical.
What surprised me was the variability. One bit length could take 100s or a couple thousand seconds even, and a product that was 1-2 bits longer could return a result in under a minute, sometimes in seconds.
This started cropping up, ironically, right after I posted the thread, whats a man to do?
So I started trying a bunch of things, some of which worked. Shameless as I am, I accepted the challenge. Things weren't perfect but it was going well enough. At that point I hadn't slept in 30~ hours so when I thought I had it I let it run and went to bed. 5 AM comes, I check the program. Still calculating, and way overshot. Fuuuuuuccc...
So here we are now and it's say to safe the worlds not gonna burn if I explain it seeing as it doesn't work, or at least only some of the time.
Others people, much smarter than me, mentioned it may be a means of finding more secure pairs, and maybe so, I'm not familiar enough to know.
For everyone that followed, commented, those who contributed, even the doubters who kept a sanity check on this without whom this would have been an even bigger embarassement, and the people with their pins and tactical dots, thanks.
So here it is.
A few assumptions first.
Assuming p = the product,
a = some prime,
b = another prime,
and r = a/b (where a is smaller than b)
w = 1/sqrt(p)
(also experimented with w = 1/sqrt(p)*2 but I kept overshooting my a very small margin)
x = a/p
y = b/p
1. for every two numbers, there is a ratio (r) that you can search for among the decimals, starting at 1.0, counting down. You can use this to find the original factors e.x. p*r=n, p/n=m (assuming the product has only two factors), instead of having to do a sieve.
2. You don't need the first number you find to be the precise value of a factor (we're doing floating point math), a large subset of decimal values for the value of a or b will naturally 'fall' into the value of a (or b) + some fractional number, which is lost. Some of you will object, "But if thats wrong, your result will be wrong!" but hear me out.
3. You round for the first factor 'found', and from there, you take the result and do p/a to get b. If 'a' is actually a factor of p, then mod(b, 1) == 0, and then naturally, a*b SHOULD equal p.
If not, you throw out both numbers, rinse and repeat.
Now I knew this this could be faster. Realized the finer the representation, the less important the fractional digits further right in the number were, it was just a matter of how much precision I could AFFORD to lose and still get an accurate result for r*p=a.
Fast forward, lot of experimentation, was hitting a lot of worst case time complexities, where the most significant digits had a bunch of zeroes in front of them so starting at 1.0 was a no go in many situations. Started looking and realized
I didn't NEED the ratio of a/b, I just needed the ratio of a to p.
Intuitively it made sense, but starting at 1.0 was blowing up the calculation time, and this made it so much worse.
I realized if I could start at r=1/sqrt(p) instead, and that because of certain properties, the fractional result of this, r, would ALWAYS be 1. close to one of the factors fractional value of n/p, and 2. it looked like it was guaranteed that r=1/sqrt(p) would ALWAYS be less than at least one of the primes, putting a bound on worst case.
The final result in executable pseudo code (python lol) looks something like the above variables plus
while w >= 0.0:
if (p / round(w*p)) % 1 == 0:
x = round(w*p)
y = p / round(w*p)
if x*y == p:
print("factors found!")
print(x)
print(y)
break
w = w + i
Still working but if anyone sees obvious problems I'd LOVE to hear about it.36 -
> be me
> has some free time
> decides to practice rust skills
> logs on codewars
> finds challenge involving prime numbers
> passes 30 min skimming the Internet to implement the Sieve Of Atkin algorithm
> tries example tests
> passes
> submits answer
> “memory allocation of 18446744073709547402 bytes. failederror: process didn’t exit successfully”
> 18446744073709547402 bytes ~= 18 million petabytes
So yeah, I think it’s broken9 -
Inspired by this post
https://devrant.com/rants/2217978/...
I challenged myself to use SQL to get the prime numbers under 100,000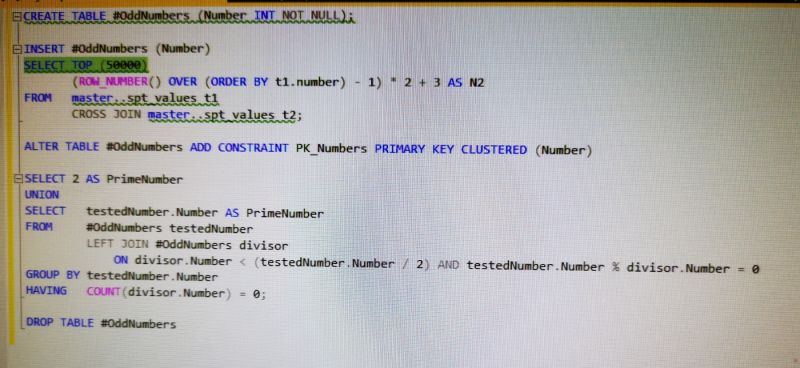 8
8 -
Two big moments today:
1. Holy hell, how did I ever get on without a proper debugger? Was debugging some old code by eye (following along and keeping track mentally, of what the variables should be and what each step did). That didn't work because the code isn't intuitive. Tried the print() method, old reliable as it were. Kinda worked but didn't give me enough fine-grain control.
Bit the bullet and installed Wing IDE for python. And bam, it hit me. How did I ever live without step-through, and breakpoints before now?
2. Remember that non-sieve prime generator I wrote a while back? (well maybe some of you do). The one that generated quasi lucas carmichael (QLC) numbers? Well thats what I managed to debug. I figured out why it wasn't working. Last time I released it, I included two core methods, genprimes() and nextPrime(). The first generates a list of primes accurately, up to some n, and only needs a small handful of QLC numbers filtered out after the fact (because the set of primes generated and the set of QLC numbers overlap. Well I think they call it an embedding, as in QLC is included in the series generated by genprimes, but not the converse, but I digress).
nextPrime() was supposed to take any arbitrary n above zero, and accurately return the nearest prime number above the argument. But for some reason when it started, it would return 2,3,5,6...but genprimes() would work fine for some reason.
So genprimes loops over an index, i, and tests it for primality. It begins by entering the loop, and doing "result = gffi(i)".
This calls into something a function that runs four tests on the argument passed to it. I won't go into detail here about what those are because I don't even remember how I came up with them (I'll make a separate post when the code is fully fixed).
If the number fails any of these tests then gffi would just return the value of i that was passed to it, unaltered. Otherwise, if it did pass all of them, it would return i+1.
And once back in genPrimes() we would check if the variable 'result' was greater than the loop index. And if it was, then it was either prime (comparatively plentiful) or a QLC number (comparatively rare)--these two types and no others.
nextPrime() was only taking n, and didn't have this index to compare to, so the prior steps in genprimes were acting as a filter that nextPrime() didn't have, while internally gffi() was returning not only primes, and QLCs, but also plenty of composite numbers.
Now *why* that last step in genPrimes() was filtering out all the composites, idk.
But now that I understand whats going on I can fix it and hypothetically it should be possible to enter a positive n of any size, and without additional primality checks (such as is done with sieves, where you have to check off multiples of n), get the nearest prime numbers. Of course I'm not familiar enough with prime number generation to know if thats an achievement or worthwhile mentioning, so if anyone *is* familiar, and how something like that holds up compared to other linear generators (O(n)?), I'd be interested to hear about it.
I also am working on filtering out the intersection of the sets (QLC numbers), which I'm pretty sure I figured out how to incorporate into the prime generator itself.
I also think it may be possible to generator primes even faster, using the carmichael numbers or related set--or even derive a function that maps one set of upper-and-lower bounds around a semiprime, and map those same bounds to carmichael numbers that act as the upper and lower bound numbers on the factors of a semiprime.
Meanwhile I'm also looking into testing the prime generator on a larger set of numbers (to make sure it doesn't fail at large values of n) and so I'm looking for more computing power if anyone has it on hand, or is willing to test it at sufficiently large bit lengths (512, 1024, etc).
Lastly, the earlier work I posted (linked below), I realized could be applied with ECM to greatly reduce the smallest factor of a large number.
If ECM, being one of the best methods available, only handles 50-60 digit numbers, & your factors are 70+ digits, then being able to transform your semiprime product into another product tree thats non-semiprime, with factors that ARE in range of ECM, and which *does* contain either of the original factors, means products that *were not* formally factorable by ECM, *could* be now.
That wouldn't have been possible though withput enormous help from many others such as hitko who took the time to explain the solution was a form of modular exponentiation, Fast-Nop who contributed on other threads, Voxera who did as well, and support from Scor in particular, and many others.
Thank you all. And more to come.
Links mentioned (because DR wouldn't accept them as they were):
https://pastebin.com/MWechZj912 -
I tried to compare Python and Julia by letting them calculate the first 200000000 prime numbers. The result is dumbfounding.
Python: 95.91282963752747 seconds
Julia: 3.84788227110 -
Teaching my homeschooled son about prime numbers, which of course means we need to also teach prime number determination in Python (his coding language of choice), when leads to a discussion of processing power, and a newly rented cloud server over at digital ocean, and a search of prime number search optimizations, questioning if python is the right language, more performance optimizations, crap, the metrics I added are slowing this down, so feature flags to toggle off the metrics, crap, I actually have a real job I need to get back to. Oooh, I'm up to prime numbers in two millions, and , oh, I really should run that ssh session in screen so it keeps running if I close my laptop. I could make this a service and let it run in the background. I bet there's a library for this. He's only 9. We've already talked about encryption and the need to find large prime numbers.2
-
I didn't leave, I just got busy working 60 hour weeks in between studying.
I found a new method called matrix decomposition (not the known method of the same name).
Premise is that you break a semiprime down into its component numbers and magnitudes, lets say 697 for example. It becomes 600, 90, and 7.
Then you break each of those down into their prime factorizations (with exponents).
So you get something like
>>> decon(697)
offset: 3, exp: [[Decimal('2'), Decimal('3')], [Decimal('3'), Decimal('1')], [Decimal('5'), Decimal('2')]]
offset: 2, exp: [[Decimal('2'), Decimal('1')], [Decimal('3'), Decimal('2')], [Decimal('5'), Decimal('1')]]
offset: 1, exp: [[Decimal('7'), Decimal('1')]]
And it turns out that in larger numbers there are distinct patterns that act as maps at each offset (or magnitude) of the product, mapping to the respective magnitudes and digits of the factors.
For example I can pretty reliably predict from a product, where the '8's are in its factors.
Apparently theres a whole host of rules like this.
So what I've done is gone an started writing an interpreter with some pseudo-assembly I defined. This has been ongoing for maybe a month, and I've had very little time to work on it in between at my job (which I'm about to be late for here if I don't start getting ready, lol).
Anyway, long and the short of it, the plan is to generate a large data set of primes and their products, and then write a rules engine to generate sets of my custom assembly language, and then fitness test and validate them, winnowing what doesn't work.
The end product should be a function that lets me map from the digits of a product to all the digits of its factors.
It technically already works, like I've printed out a ton of products and eyeballed patterns to derive custom rules, its just not the complete set yet. And instead of spending months or years doing that I'm just gonna finish the system to automatically derive them for me. The rules I found so far have tested out successfully every time, and whether or not the engine finds those will be the test case for if the broader system is viable, but everything looks legit.
I wouldn't have persued this except when I realized the production of semiprimes *must* be non-eularian (long story), it occured to me that there must be rich internal representations mapping products to factors, that we were simply missing.
I'll go into more details in a later post, maybe not today, because I'm working till close tonight (won't be back till 3 am), but after 4 1/2 years the work is bearing fruit.
Also, its good to see you all again. I fucking missed you guys.9 -
CONTEST - Win big $$$ straight from Wisecrack!
For all those who participated in my original "cracking prime factorization" thread (and several I decided to add just because), I'm offering a whopping $5 to anyone who posts a 64 bit *product* of two primes, which I cant factor. Partly this is a thank you for putting up with me.
FIVE WHOLE DOLLARS! In 1909 money thats $124 dollars! Imagine how many horse and buggy rides you could buy with that back then! Or blowjobs!
Probably not a lot!
But still.
So the contest rules are simple:
Go to
https://asecuritysite.com/encryptio...
Enter 32 for the number of bits per prime, and generate a 64 bit product.
Post it here to enter the contest.
Products must be 64 bits, and the result of just *two* prime numbers. Smaller or larger bit lengths for products won't be accepted at this time.
I'm expecting a few entries on this. Entries will generally be processed in the order of submission, but I reserve the right to wave this rule.
After an entry is accepted, I'll post "challenge accepted. Factoring now."
And from that point on I have no more than 5 hours to factor the number, (but results usually arrive in 30-60 minutes).
If I fail to factor your product in the specified time (from the moment I indicate I've begun factoring), congratulations, you just won $5.
Payment will be made via venmo or other method at my discretion.
One entry per user. Participants from the original thread only, as well as those explicitly mentioned.
Limitations: Factoring shall be be done
1. without *any* table lookup of primes or equivalent measures, 2. using anything greater than an i3, 3. without the aid of a gpu, 4. without multithreading. 5. without the use of more than one machine.
FINALLY:
To claim your prize, post the original factors of your product here, after the deadline has passed.
And then I'll arrange payment of the prize.
You MUST post the factors of your product after the deadline, to confirm your product and claim your prize.99 -
I think I did it. I did the thing I set out to do.
let p = a semiprime of simple factors ab.
let f equal the product of b and i=2...a inclusive, where i is all natural numbers from 2 to a.
let s equal some set of prime factors that are b-smooth up to and including some factor n, with no gaps in the set.
m is a the largest primorial such that f%m == 0, where
the factors of s form the base of a series of powers as part of a product x
1. where (x*p) = f
2. and (x*p)%f == a
if statement 2 is untrue, there still exists an algorithm that
3. trivially derives the exponents of s for f, where the sum of those exponents are less than a.
4. trivially generates f from p without knowing a and b.
For those who have followed what I've been trying to do for so long, and understand the math,
then you know this appears to be it.
I'm just writing and finishing the scripts for it now.
Thank god. It's just in time. Maybe we can prevent the nuclear apocalypse with the crash this will cause if it works.2 -
Hey, been gone a hot minute from devrant, so I thought I'd say hi to Demolishun, atheist, Lensflare, Root, kobenz, score, jestdotty, figoore, cafecortado, typosaurus, and the raft of other people I've met along the way and got to know somewhat.
All of you have been really good.
And while I'm here its time for maaaaaaaaath.
So I decided to horribly mutilate the concept of bloom filters.
If you don't know what that is, you take two random numbers, m, and p, both prime, where m < p, and it generate two numbers a and b, that output a function. That function is a hash.
Normally you'd have say five to ten different hashes.
A bloom filter lets you probabilistic-ally say whether you've seen something before, with no false negatives.
It lets you do this very space efficiently, with some caveats.
Each hash function should be uniformly distributed (any value input to it is likely to be mapped to any other value).
Then you interpret these output values as bit indexes.
So Hi might output [0, 1, 0, 0, 0]
while Hj outputs [0, 0, 0, 1, 0]
and Hk outputs [1, 0, 0, 0, 0]
producing [1, 1, 0, 1, 0]
And if your bloom filter has bits set in all those places, congratulations, you've seen that number before.
It's used by big companies like google to prevent re-indexing pages they've already seen, among other things.
Well I thought, what if instead of using it as a has-been-seen-before filter, we mangled its purpose until a square peg fit in a round hole?
Not long after I went and wrote a script that 1. generates data, 2. generates a hash function to encode it. 3. finds a hash function that reverses the encoding.
And it just works. Reversible hashes.
Of course you can't use it for compression strictly, not under normal circumstances, but these aren't normal circumstances.
The first thing I tried was finding a hash function h0, that predicts each subsequent value in a list given the previous value. This doesn't work because of hash collisions by default. A value like 731 might map to 64 in one place, and a later value might map to 453, so trying to invert the output to get the original sequence out would lead to branching. It occurs to me just now we might use a checkpointing system, with lookahead to see if a branch is the correct one, but I digress, I tried some other things first.
The next problem was 1. long sequences are slow to generate. I solved this by tuning the amount of iterations of the outer and inner loop. We find h0 first, and then h1 and put all the inputs through h0 to generate an intermediate list, and then put them through h1, and see if the output of h1 matches the original input. If it does, we return h0, and h1. It turns out it can take inordinate amounts of time if h0 lands on a hash function that doesn't play well with h1, so the next step was 2. adding an error margin. It turns out something fun happens, where if you allow a sequence generated by h1 (the decoder) to match *within* an error margin, under a certain error value, it'll find potential hash functions hn such that the outputs of h1 are *always* the same distance from their parent values in the original input to h0. This becomes our salt value k.
So our hash-function generate called encoder_decoder() or 'ed' (lol two letter functions), also calculates the k value and outputs that along with the hash functions for our data.
This is all well and good but what if we want to go further? With a few tweaks, along with taking output values, converting to binary, and left-padding each value with 0s, we can then calculate shannon entropy in its most essential form.
Turns out with tens of thousands of values (and tens of thousands of bits), the output of h1 with the salt, has a higher entropy than the original input. Meaning finding an h1 and h0 hash function for your data is equivalent to compression below the known shannon limit.
By how much?
Approximately 0.15%
Of course this doesn't factor in the five numbers you need, a0, and b0 to define h0, a1, and b1 to define h1, and the salt value, so it probably works out to the same. I'd like to see what the savings are with even larger sets though.
Next I said, well what if we COULD compress our data further?
What if all we needed were the numbers to define our hash functions, a starting value, a salt, and a number to represent 'depth'?
What if we could rearrange this system so we *could* use the starting value to represent n subsequent elements of our input x?
And thats what I did.
We break the input into blocks of 15-25 items, b/c thats the fastest to work with and find hashes for.
We then follow the math, to get a block which is
H0, H1, H2, H3, depth (how many items our 1st item will reproduce), & a starting value or 1stitem in this slice of our input.
x goes into h0, giving us y. y goes into h1 -> z, z into h2 -> y, y into h3, giving us back x.
The rest is in the image.
Anyway good to see you all again. 20
20 -
I got pranked. I got pranked good.
My prof at my uni had given us an asigment to do in java for a class.
Easy peasy for me, it was only a formality...
First task was normal but...
The second one included making a random number csv gen with the lenght of at least 10 digits, a class for checking which numbers are a prime or not and a class that will check numbers from that cvs and create a new cvs with only primes in it. I have created the code and only when my fans have taken off like a jet i realised... I fucked up...
In that moment i realised that prime checking might... take a while..
There was a third task but i didnt do it for obvious reasons. He wanted us to download a test set of few text files and make a csv with freq of every word in that test set. The problem was... The test set was a set of 200 literature books...17 -
Found a clever little algorithm for computing the product of all primes between n-m without recomputing them.
We'll start with the product of all primes up to some n.
so [2, 2*3, 2*3*5, 2*3*5*,7..] etc
prods = []
i = 0
total = 1
while i < 100:
....total = total*primes[i]
....prods.append(total)
....i = i + 1
Terrible variable names, can't be arsed at the moment.
The result is a list with the values
2, 6, 30, 210, 2310, 30030, etc.
Now assume you have two factors,with indexes i, and j, where j>i
You can calculate the gap between the two corresponding primes easily.
A gap is defined at the product of all primes that fall between the prime indexes i and j.
To calculate the gap between any two primes, merely look up their index, and then do..
prods[j-1]/prods[i]
That is the product of all primes between the J'th prime and the I'th prime
To get the product of all primes *under* i, you can simply look it up like so:
prods[i-1]
Incidentally, finding a number n that is equivalent to (prods[j+i]/prods[j-i]) for any *possible* value of j and i (regardless of whether you precomputed n from the list generator for prods, or simply iterated n=n+1 fashion), is equivalent to finding an algorithm for generating all prime numbers under n.
Hypothetically you could pick a number N out of a hat, thats a thousand digits long, and it happens to be the product of all primes underneath it.
You could then start generating primes by doing
i = 3
while i < N:
....if (N/k)%1 == 0:
........factors.append(N/k)
....i=i+1
The only caveat is that there should be more false solutions as real ones. In otherwords theres no telling if you found a solution N corresponding to some value of (prods[j+i]/prods[j-i]) without testing the primality of *all* values of k under N.13 -
Hey fellas, especially you security nerds.
I've had asymmetric encryption explained to me a number of times but I can't get a handle on it because no example actually talks in human terms. They always say "two enormous prime numbers", which I understand, but I can't conceptualize.
Can someone walk me through an entire process, showing your math & work, using some very small, single- or double-digit primes? Such as if I were to encrypt the text "hello world" using prime numbers like 3, 5, and 710 -
Following on from my previous SQL script to find prime numbers
https://devrant.com/rants/2218452/...
I wondered whether there was a way to improve it by only checking for prime factors. It feels really dirty to use a WHILE loop in SQL, but I couldn't think of another way to incrementally use the already found prime numbers when checking for prime factors.
It's fast though, 2 mins 15 seconds for primes under 1,000,000 - previous query took over an hour and a half. 5
5 -
In the 90s most people had touched grass, but few touched a computer.
In the 2090s most people will have touched a computer, but not grass.
But at least we'll have fully sentient dildos armed with laser guns to mildly stimulate our mandatory attached cyber-clits, or alternatively annihilate thought criminals.
In other news my prime generator has exhaustively been checked against, all primes from 5 to 1 million. I used miller-rabin with k=40 to confirm the results.
The set the generator creates is the join of the quasi-lucas carmichael numbers, the carmichael numbers, and the primes. So after I generated a number I just had to treat those numbers as 'pollutants' and filter them out, which was dead simple.
Whats left after filtering, is strictly the primes.
I also tested it randomly on 50-55 bit primes, and it always returned true, but that range hasn't been fully tested so far because it takes 9-12 seconds per number at that point.
I was expecting maybe a few failures by my generator. So what I did was I wrote a function, genMillerTest(), and all it does is take some number n, returns the next prime after it (using my functions nextPrime() and isPrime()), and then tests it against miller-rabin. If miller returns false, then I add the result to a list. And then I check *those* results by hand (because miller can occasionally return false positives, though I'm not familiar enough with the math to know how often).
Well, imagine my surprise when I had zero false positives.
Which means either my code is generating the same exact set as miller (under some very large value of n), or the chance of miller (at k=40 tests) returning a false positive is vanishingly small.
My next steps should be to parallelize the checking process, and set up my other desktop to run those tests continuously.
Concurrently I should work on figuring out why my slowest primality tests (theres six of them, though I think I can eliminate two) are so slow and if I can better estimate or derive a pattern that allows faster results by better initialization of the variables used by these tests.
I already wrote some cases to output which tests most frequently succeeded (if any of them pass, then the number isn't prime), and therefore could cut short the primality test of a number. I rewrote the function to put those tests in order from most likely to least likely.
I'm also thinking that there may be some clues for faster computation in other bases, or perhaps in binary, or inspecting the patterns of values in the natural logs of non-primes versus primes. Or even looking into the *execution* time of numbers that successfully pass as prime versus ones that don't. Theres a bevy of possible approaches.
The entire process for the first 1_000_000 numbers, ran 1621.28 seconds, or just shy of a tenth of a second per test but I'm sure thats biased toward the head of the list.
If theres any other approach or ideas I may be overlooking, I wouldn't know where to begin.16 -
Maybe I'm severely misunderstanding set theory. Hear me out though.
Let f equal the set of all fibonacci numbers, and p equal the set of all primes.
If the density of primes is a function of the number of *multiples* of all primes under n,
then the *number of primes* or density should shrink as n increases, at an ever increasing rate
greater than the density of the number of fibonacci numbers below n.
That means as n grows, the relative density of f to p should grow as well.
At sufficiently large n, the density of p is zero (prime number theorem), not just absolutely, but relative to f as well. The density of f is therefore an upper limit of the density of p.
And the density of p given some sufficiently large n, is therefore also a lower limit on the density of f.
And that therefore the density of p must also be the upper limit on the density of the subset of primes that are Fibonacci numbers.
WHICH MEANS at sufficiently large values of n, there are either NO Fibonacci primes (the functions diverge), and therefore the set of Fibonacci primes is *finite*, OR the density of primes given n in the prime number theorem
*never* truly reaches zero, meaning the primes are in fact infinite.
Proving the Fibonacci primes are infinite, therefore would prove that the prime number line ends (fat chance). While proving the primes are infinite, proves the Fibonacci primes are finite in quantity.
And because the number of primes has been proven time and again to be infinite, as far back as 300BC,the Fibonacci primes MUST be finite.
QED.
If I've made a mistake, I'd like to know.11 -
Officially faster bruteforcing:
https://pastebin.com/uBFwkwTj
Provided toy values for others to try. Haven't tested if it works with cryptographic secure prime pairs (gcf(p, q) == 1)
It's a 50% reduction in time to bruteforce a semiprime. But I also have some inroads to a/30.
It's not "broke prime factorization for good!" levels of fast, but its still pretty nifty.
Could use decimal support with higher precision so I don't cause massive overflows on larger numbers, but this is just a demonstration after all.10 -
I learned to program with the joy of the command line and ASCII rocket ships printed and shell games on GWBasic. It was fat spiral bound manual my Dad gave me when he worked at EDS. My dad then tried to press me to leaning a program for calculating prime and perfect numbers. My dad sort of forgot I was only six and hadn't learned division yet.1
-
Free to good home.
https://store.steampowered.com/app/...
Code: B85LX-ITFZR-GB3P
If you can guess the last digit you can have it. 9
9 -
Up all damn night making the script work.
Wrote a non-sieve prime generator.
Thing kept outputting one or two numbers that weren't prime, related to something called carmichael numbers.
Any case got it to work, god damn was it a slog though.
Generates next and previous primes pretty reliably regardless of the size of the number
(haven't gone over 31 bit because I haven't had a chance to implement decimal for this).
Don't know if the sieve is the only reliable way to do it. This seems to do it without a hitch, and doesn't seem to use a lot of memory. Don't have to constantly return to a lookup table of small factors or their multiple either.
Technically it generates the primes out of the integers, and not the other way around.
Things 0.01-0.02th of a second per prime up to around the 100 million mark, and then it gets into the 0.15-1second range per generation.
At around primes of a couple billion, its averaging about 1 second per bit to calculate 1. whether the number is prime or not, 2. what the next or last immediate prime is. Although I'm sure theres some optimization or improvement here.
Seems reliable but obviously I don't have the resources to check it beyond the first 20k primes I confirmed.
From what I can see it didn't drop any primes, and it didn't include any errant non-primes.
Codes here:
https://pastebin.com/raw/57j3mHsN
Your gotos should be nextPrime(), lastPrime(), isPrime, genPrimes(up to but not including some N), and genNPrimes(), which generates x amount of primes for you.
Speed limit definitely seems to top out at 1 second per bit for a prime once the code is in the billions, but I don't know if thats the ceiling, again, because decimal needs implemented.
I think the core method, in calcY (terrible name, I know) could probably be optimized in some clever way if its given an adjacent prime, and what parameters were used. Theres probably some pattern I'm not seeing, but eh.
I'm also wondering if I can't use those fancy aberrations, 'carmichael numbers' or whatever the hell they are, to calculate some sort of offset, and by doing so, figure out a given primes index.
And all my brain says is "sleep"
But family wants me to hang out, and I have to go talk a manager at home depot into an interview, because wanting to program for a living, and actually getting someone to give you the time of day are two different things.1 -
So I promised a post after work last night, discussing the new factorization technique.
As before, I use a method called decon() that takes any number, like 697 for example, and first breaks it down into the respective digits and magnitudes.
697 becomes -> 600, 90, and 7.
It then factors *those* to give a decomposition matrix that looks something like the following when printed out:
offset: 3, exp: [[Decimal('2'), Decimal('3')], [Decimal('3'), Decimal('1')], [Decimal('5'), Decimal('2')]]
offset: 2, exp: [[Decimal('2'), Decimal('1')], [Decimal('3'), Decimal('2')], [Decimal('5'), Decimal('1')]]
offset: 1, exp: [[Decimal('7'), Decimal('1')]]
Each entry is a pair of numbers representing a prime base and an exponent.
Now the idea was that, in theory, at each magnitude of a product, we could actually search through the *range* of the product of these exponents.
So for offset three (600) here, we're looking at
2^3 * 3 ^ 1 * 5 ^ 2.
But actually we're searching
2^3 * 3 ^ 1 * 5 ^ 2.
2^3 * 3 ^ 1 * 5 ^ 1
2^3 * 3 ^ 1 * 5 ^ 0
2^3 * 3 ^ 0 * 5 ^ 2.
2^3 * 3 ^ 1 * 5 ^ 1
etc..
On the basis that whatever it generates may be the digits of another magnitude in one of our target product's factors.
And the first optimization or filter we can apply is to notice that assuming our factors pq=n,
and where p <= q, it will always be more efficient to search for the digits of p (because its under n^0.5 or the square root), than the larger factor q.
So by implication we can filter out any product of this exponent search that is greater than the square root of n.
Writing this code was a bit of a headache because I had to deal with potentially very large lists of bases and exponents, so I couldn't just use loops within loops.
Instead I resorted to writing a three state state machine that 'counted down' across these exponents, and it just works.
And now, in practice this doesn't immediately give us anything useful. And I had hoped this would at least give us *upperbounds* to start our search from, for any particular digit of a product's factors at a given magnitude. So the 12 digit (or pick a magnitude out of a hat) of an example product might give us an upperbound on the 2's exponent for that same digit in our lowest factor q of n.
It didn't work out that way. Sometimes there would be 'inversions', where the exponent of a factor on a magnitude of n, would be *lower* than the exponent of that factor on the same digit of q.
But when I started tearing into examples and generating test data I started to see certain patterns emerge, and immediately I found a way to not just pin down these inversions, but get *tight* bounds on the 2's exponents in the corresponding digit for our product's factor itself. It was like the complications I initially saw actually became a means to *tighten* the bounds.
For example, for one particular semiprime n=pq, this was some of the data:
n - offset: 6, exp: [[Decimal('2'), Decimal('5')], [Decimal('5'), Decimal('5')]]
q - offset: 6, exp: [[Decimal('2'), Decimal('6')], [Decimal('3'), Decimal('1')], [Decimal('5'), Decimal('5')]]
It's almost like the base 3 exponent in [n:7] gives away the presence of 3^1 in [q:6], even
though theres no subsequent presence of 3^n in [n:6] itself.
And I found this rule held each time I tested it.
Other rules, not so much, and other rules still would fail in the presence of yet other rules, almost like a giant switchboard.
I immediately realized the implications: rules had precedence, acted predictable when in isolated instances, and changed in specific instances in combination with other rules.
This was ripe for a decision tree generated through random search.
Another product n=pq, with mroe data
q(4)
offset: 4, exp: [[Decimal('2'), Decimal('4')], [Decimal('5'), Decimal('3')]]
n(4)
offset: 4, exp: [[Decimal('2'), Decimal('3')], [Decimal('3'), Decimal('2')], [Decimal('5'), Decimal('3')]]
Suggesting that a nontrivial base 3 exponent (**2 rather than **1) suggests the exponent on the 2 in the relevant
digit of [n], is one less than the same base 2 digital exponent at the same digit on [q]
And so it was clear from the get go that this approach held promise.
From there I discovered a bunch more rules and made some observations.
The bulk of the patterns, regardless of how large the product grows, should be present in the smaller bases (some bound of primes, say the first dozen), because the bulk of exponents for the factorization of any magnitude of a number, overwhelming lean heavily in the lower prime bases.
It was if the entire vulnerability was hiding in plain sight for four+ years, and we'd been approaching factorization all wrong from the beginning, by trying to factor a number, and all its digits at all its magnitudes, all at once, when like addition or multiplication, factorization could be done piecemeal if we knew the patterns to look for.7 -
I'm looking for more semiprimes to test my code on, regardless of the bit length, up to a reasonable number of 2048 bits because the code is unoptimized.
For those wanting to see for themselves if its more failed efforts, heres what you can do to help:
1. post a semiprime
2. optionally post a hash of one of the factors to confirm it.
3. I'll respond within the hour with a set of numbers that contain the first three digits of p and the first three digits of q.
4. After I post my answer, you post the correct answer so others can confirm it is working.
How this works:
All factors of semiprimes can be characterized by a partial factorization of n digits.
If you have a pair of primes like q=79926184211, and p=15106381891, the k=3 pair would be [151, 799]
The set of all digits of this kind is 810,000 pairs.
My answers can be no larger than 2000 pairs, and are guaranteed to contain the partial factorization regardless of the bit length of n.
I especially encourage you to participate if you never thought for a second that the RSA research I've been doing on and off for a few years was ever real.
But those who enjoyed it and thought there might be something to it, if you want to come have fun, or poke fun, I encourage you to post some numbers too!
Semiprimes only.
Keys can be any size up to 2048 bits.
But I won't take any keys under 24 bits, and none over 2048.
You should be able to prove after the fact you know p and q, not only so everyone can confirm the results for themselves, but also because I don't want anyone getting cheeky and posting say the public key to a bank or google or something.
Good luck, lets see if you got a number I can't crack.
For prime numbers you're welcome to use
https://bigprimes.org/
... or any other source you prefer.25 -
!rant
Just posted some swift code to a server, in a few hours I should have all the prime numbers from 1 to a billion!2 -
What's your first instance of a infinite loop which ended badly?
Mine was a loop to calculate prime numbers.
My computer came to a halt within 5 seconds :S4 -
all video streaming fucker companies have found a new way to promote shitty lies!
Hotstar: "try Hotstar! Rs199/month! first 7days free!"
Amazon prime : "try amazon prime! Rs 129/month! first 30 days free!"
those small numbers are fuckin lies. they have only 2 or 3 supported banks and if yours isn't one of them, then you have no option but to buy their full 365 days non refundable subscription of a larger amount, which strangely accepts *all payment bank cards*
liars. liar liar liars! 7
7 -
Well fuck Amazon. I am trying to get into my account because for some fucking reason they say my payment method is faulty while they actually write off the subscription of prime of it. But to get into my account I need to login again with 2FA as I have that turned it on. So far so good. But since it's an old phone number I can't login. Well just change the phone number wouldn't you think? Well yes but to change the phone number I need to login in with the old phone number to which I have no longer access 🤦♂️. Eventually found a phone number I could call. I get a lovely lady on the phone which guides me to resetting my password but for that, you guessed it, I need to do the 2FA again. I get send through to the next person as she can't change it for me because of privacy reasons (oh well). That guy first askes the last 4 numbers of my creditcard like 5 times because he can't remember it (write it the fuck down then asshole) then he starts mistaking the 6 for 9 (like how the fuck do you do that) and then the text messages don't come in while I am on the phone with him which he tries to blame to my service provider because they would block Amazon (like why would they do that?). But since I got a text message of them 15 min before I shot that down quickly. Then he finally admitted that they might have a disruption going on. So I think we'll fine I'll just ask my question to him how it's possible that Prime stops working as I am watching it because my payment method is faulty according to them (but manage to write off the subscription) and he starts talking just shit. Just admit that you don't know and connect me to someone who does know how that can happen. In the the end I just hung up because I knew I wasn't getting anywhere with this guy and don't you know it, as I start writing this the text messages come in. Problem solved you would say just out that number in the website and you can change your phone number. Well no because I have to tell the number to the guy who I hung up with because the texts weren't coming in 😒. Now I should call them back but I think I'll wait till tomorrow hopefully the day shift will be a bit more knowledgeable on how shit works and can actually remember 4 digits.2
-
Partially week 69: I wish I could stop getting distracted by toy problems. Mostly the collatz conjecture. Or counting in prime numbers.
-
Heres the initial upgraded number fingerprinter I talked about in the past and some results and an explanation below.
Note that these are wide black images on ibb, so they appear as a tall thin strip near the top of ibb as if they're part of the website. They practically blend in. Right click the blackstrip and hit 'view image' and then zoom in.
https://ibb.co/26JmZXB
https://ibb.co/LpJpggq
https://ibb.co/Jt2Hsgt
https://ibb.co/hcxrFfV
https://ibb.co/BKZNzng
https://ibb.co/L6BtXZ4
https://ibb.co/yVHZNq4
https://ibb.co/tQXS8Hr
https://paste.ofcode.org/an4LcpkaKr...
Hastebin wouldn't save for some reason so paste.ofcode.org it is.
Not much to look at, but I was thinking I'd maybe mark the columns where gaps occur and do some statistical tests like finding the stds of the gaps, density, etc. The type test I wrote categorizes products into 11 different types, based on the value of a subset of variables taken from a vector of a couple hundred variables but I didn't want to include all that mess of code. And I was thinking of maybe running this fingerprinter on a per type basis, set to repeat, and looking for matching indexs (pixels) to see what products have in common per type.
Or maybe using them to train a classifier of some sort.
Each fingerprint of a product shares something like 16-20% of indexes with it's factors, so I'm thinking thats an avenue to explore.
What the fingerprinter does is better explained by the subfunction findAb.
The code contains a comment explaining this, but basically the function destructures a number into a series of division and subtractions, and makes a note of how many divisions in a 'run'.
Typically this is for numbers divisible by 2.
So a number like 35 might look like this, when done
p = 35
((((p-1)/2)-1)/2/2/2/2)-1
And we'd represent that as
ab(w, x, y, z)
Where w is the starting value 35 in this case,
x is the number to divide by at each step, y is the adjustment (how much to subtract by when we encounter a number not divisible by x), and z is a string or vector of our results
which looks something like
ab(35, 2, 1, [1, 4])
Why [1,4]
because we were only able to divide by 2 once, before having to subtract 1, and repeat the process. And then we had a run of 4 divisions.
And for the fingerprinter, we do this for each prime under our number p, the list returned becoming another row in our fingerprint. And then that gets converted into an image.
And again, what I find interesting is that
unknown factors of products appear to share many of these same indexes.
What I might do is for, each individual run of Ab, I might have some sort of indicator for when *another* factor is present in the current factor list for each index. So I might ask, at the given step, is the current result (derived from p), divisible by 2 *and* say, 3? If so, mark it.
And then when I run this through the fingerprinter itself, all those pixels might get marked by a different color, say, make them blue, or vary their intensity based on the number of factors present, I don't know. Whatever helps the untrained eye to pick up on leads, clues, and patterns.
If it doesn't make sense, take another look at the example:
((((p-1)/2)-1)/2/2/2/2)-1
This is semi-unique to each product. After the fact, you can remove the variable itself, and keep just the structure in question, replacing the first variable with some other number, and you get to see what pops out the otherside.
If it helps, you can think of the structure surrounding our variable p as the 'electron shell', the '-1's as bandgaps, and the runs of '2's as orbitals, with the variable at the center acting as the 'nucleus', with the factors of that nucleus acting as the protons and neutrons, or nougaty center lol.
Anyway I just wanted to share todays flavor of insanity on the off chance someone might enjoy reading it.1 -
1. Went to try chat.openai.com/chat
2. "Write a java program that uses a singleon pattern to calculate the sum of the first 100 prime numbers"
3. ???? HOW DOES IT DO THAT8 -
create two function one for finding factorial of first 6 prime numbers and another for storing prime numbers and their factorial in two separate arrays. call both the function inside the main function.write a c++ code for solving this problem and displaying the all desired output.4
-
Most painful code!!
Well , it was to write a code in 'C' which will print first N times prime numbers. As a noob , it was really very painful.5


