Join devRant
Do all the things like
++ or -- rants, post your own rants, comment on others' rants and build your customized dev avatar
Sign Up
Pipeless API

From the creators of devRant, Pipeless lets you power real-time personalized recommendations and activity feeds using a simple API
Learn More
Search - "fibonacci"
-
Knock.
Knock.
Knock knock.
Knock knock knock.
Knock knock knock knock knock.
Who's there?
Fibonacci.5 -
Update on this: https://devrant.com/rants/1641198/...
I was a little tired but made updated and currently getting a more natural looking tree.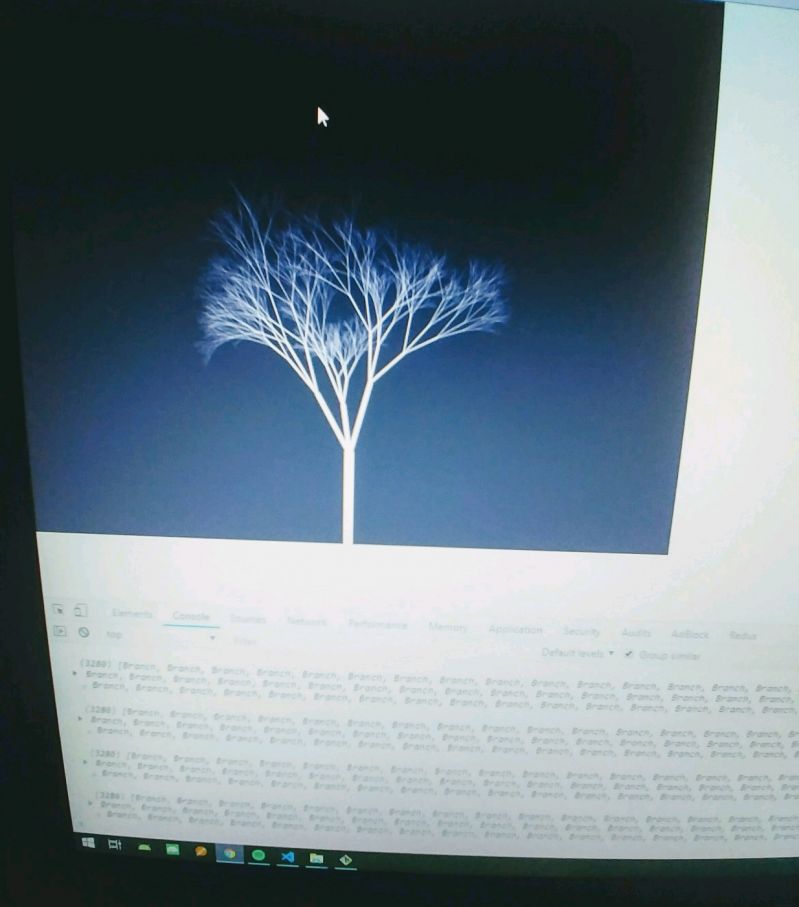 24
24 -
Not having finished any education, and writing code during interviews.
I have a pretty nice resume with good references, and I think I'm a reasonably good & experienced dev.
But I'm absolutely unable to write code on paper, and really wonder how some devs can just write out algorithms using a pen and reason about it, without trying/failing/playing/fixing in an IDE.
Education I think.
I can transform the theory on a complex Wikipedia page about math/algorithm into code, I can translate a Haskell library into idiomatic python... but what I haven't done is write out sorting functions or fibonacci generators a million times during Java class.
I don't see the point either... but I still feel utterly worthless during an interview if they ask "So you haven't even finished highschool? Can you at least solve this prime number problem using a marker on this whiteboard? Could you explain in words which sorting algorithm is faster and why?"
"Uh... let me fetch a laptop with an IDE, stackoverflow and Wikipedia?"22 -
Teacher: Write a program to print fibonacci series up to 8 terms
Me: *hardcodes 0,1,1,2,3,5,8,13*
Teacher: *runs the programs*
Me: *relieved*
Teacher: *checks the code*
Me: 5
5 -
Fibonacci for developers.
One Developer writes bad code and leaves. Company hires two more to fix the code and cycle continues. Now you know why software developers are in demand.2 -
At a job interview.
Them: Can you please write a function that calculates fibonacci numbers on the whiteboard please.
Me:
fib=_=>($=>$.round(($.pow((1+$.sqrt(5))/2,_)-$.pow(-2/(1+$.sqrt(5)),_))/$.sqrt(5)))(Math)17 -
In the first lesson on the school the teacher mentioned the fibonaci formula, and because I already had a little experience in programming I wrote a program witch outputs a given amount of numbers after the Fibonacci formula and showed it to the teacher who didn't really showed any reaction. At the end of my time in the school while the exams preparation he told us that last year one part of the exam was to program for the Fibonacci formula. At this point I realized that my little experience in programming was already to much for the class and why I did not learn any thing in 2 years.
Ps: sry for my bad English.1 -
My uncle introduced me to basic and used to challenge me to solve problems. One day he challenged me to write a program that generates the Fibonacci series. Thirty minutes later I had the solution and was irrevocably hooked :)
-
!rant
... so... maybe not that much of a thing, but i think it is:
a gal (27 years old) i started teaching programming two weeks ago, who had literally no previous experience with programming, algoritmization nor c#...
... just now, after 3 lessons of 6 hours altogether, and after yesterday when i explained to her what arrays are and reminded her what loops do...
... invented bubble sort. on her own. no googling. on paper. no "trial and error code typing and running".
i'm actually pretty proud of her :)
... putting the algo concept into actual code will still be a bit of a struggle, but yeah, hell, can't help thinking that she's actually pretty smart :)
(p. s. fist lesson was i drew uml of a fibonacci algo and forced her to understand what it does, second lesson was i explained the minimum required c# syntax for her to be able to implement it and forced her to write it (with as little help as i could), third lesson was the concept of array and "okay, now here's array of numbers, make a function that will sort them")
looking forward to what will happen when i explain recursion and nudge her towards quicksort O:-)8 -
"While the number of rabbits grows, the rabbits will grow in number."
Teacher explaining the Fibonacci sequence.2 -
Meet today.... Fetlang
---
lick Bob's cock
lick Duke's left nipple one million times
while Ada is submissive to Duke
make slave scream Ada's name
Have Charlie spank himself
Have Ada lick his tight little ass
Have Bob lick Charlie's tight little ass, as well
make Ada moan Bob's name
make Bob moan Charlie's name
---
Never felt so dirty after calculating the fibonacci sequence...
https://github.com/Property404/...
"Fetlang is a statically typed, procedural, esoteric programming language and reference implementation. It is designed such that source code looks like poorly written fetish erotica."8 -
I started learning ASM x86_64, so I chose MASM with VS 2013 because is the best for debugging
So I just waste like 2 hours trying to make a simple program like printing fibonacci numbers to start with ASM
The problem started when using printf function, after calling printf function, local vars became garbage, after googling and looking for the ultimate answer for the problem I found the site with the ultimate answer (https://cs.uaf.edu/2017/fall/...) and it was that MASM64 when calling a function you must allocate space with the actual space from the current function + the allocated space for the printf11 -
Software Engg here, applying for PhD after working 2 yrs @top5 giants.
Everyone is saying, without any "research experience", I stand ZERO chance of admission.
So, I'm expected to leave my 7 figure job, be someone's bitch for 6m to get a paper , and then maybe, JUST maybe I will be eligible for admission. WHY CAN'T I JUST LEARN IN THE 1ST YEAR OF PhD ?
STUPID MOTHERFUCKERS FROM ALL OVER THE WORLD GET INTO PhD ALL THE TIME. EVEN SOMEONE WHO CANT CODE FIBONACCI USING DP, GETS IN BY SHOWING FAKE RECO LETTERS(CASH), HIGH GPA (GATHERED BY LICKING EVERY TEACHER'S ASS), AND "RESEARCH EXPERIENCE" FROM PRIVATE UNIVERSITY BECAUSE THEY ARE TOOOO DUMB TO GEY INTO GOVT UNIVERSITY . (Seen myself)
I SWEAR TO GOD, IF I Don't get into PhD, this year, I'll probably loose my shit.10 -
Jeff Dean Facts (Source: God)
Jeff Dean once failed a Turing test when he correctly identified the 203rd Fibonacci number in less than a second
Jeff Dean compiles and runs his code before submitting, but only to check for compiler and CPU bugs
Unsatisfied with constant time, Jeff Dean created the world's first O(1/n) algorithm
When Jeff Dean designs software, he first codes the binary and then writes the source as documentation
Compilers don't warn Jeff Dean. Jeff Dean warns compilers
Jeff Dean wrote an O(n^2) algorithm once. It was for the Traveling Salesman Problem
Jeff Dean's watch displays seconds since January 1st, 1970.
gcc -O4 sends your code to Jeff Dean for a complete rewrite
-
The Fibonacci sequence also known as he fingerprint of God is the most efficient memory maintenance method in computing as well
#weirdcode11 -
I just found something cool on accident.
Assuming you start the fibonacci sequence on 2, you can find any of the fibonacci numbers for a given index with a simple trick:
Let Phi = 1.618
Let your index n = n+1
Floor(phi**(n+1+0.328))+1 = the fibonacci number at index n in the sequence.
This probably breaks down past some point but its nifty.21 -
Other than the obligatory “Hello World”, what was the first program you had ever written, Personally and also Professionally?
For me...
PERSONALLY: Fibonacci Calculator.
PROFESSIONALLY: Menu System.7 -
Doesn’t everybody use Fibonacci story dev points to estimate stories?
Doesn’t.. everybody..? 😞
😭😭😭😭😭😭😭6 -
My first job as a '"dev"' (I really need some kind of super quotation mark for this).
I was young and too stupid too know how stupid I really was, I jobbed at a small recruiting firm and one day my boss complained about her database system and that she needed to hire a student to remake it. Suffering from the problem to be too incompetent to even recognise I'm incompetent I obviously offered my services as a python wizard I mean I could write a program that saves fibonacci numbers to a csv file, how much more could there possibly be? Fast forward two months and I proudly presented a GUI written in VB (it had an wysiwyg GUI editor) that was loosely frankensteined onto a bunch of together copy pasted python scripts running on a Windows Server. No web interface just accessible via vnc. It was slow, sluggish and soo ugly but it worked and did exactly what she wanted it to do. Sure the database was a bunch of csv files but non the less, to say it in pm, it resolved the user story. I quit shortly after because of her tendency to not pay the last bill after something was done (and tbh i deserved it) but she never removed my account from the server. So I copied my "magnus opus" from there... Let's just say whenever I look back at it I feel ashamed and yet it serves as a reminder to never be content with how good you are. -
Maybe I'm severely misunderstanding set theory. Hear me out though.
Let f equal the set of all fibonacci numbers, and p equal the set of all primes.
If the density of primes is a function of the number of *multiples* of all primes under n,
then the *number of primes* or density should shrink as n increases, at an ever increasing rate
greater than the density of the number of fibonacci numbers below n.
That means as n grows, the relative density of f to p should grow as well.
At sufficiently large n, the density of p is zero (prime number theorem), not just absolutely, but relative to f as well. The density of f is therefore an upper limit of the density of p.
And the density of p given some sufficiently large n, is therefore also a lower limit on the density of f.
And that therefore the density of p must also be the upper limit on the density of the subset of primes that are Fibonacci numbers.
WHICH MEANS at sufficiently large values of n, there are either NO Fibonacci primes (the functions diverge), and therefore the set of Fibonacci primes is *finite*, OR the density of primes given n in the prime number theorem
*never* truly reaches zero, meaning the primes are in fact infinite.
Proving the Fibonacci primes are infinite, therefore would prove that the prime number line ends (fat chance). While proving the primes are infinite, proves the Fibonacci primes are finite in quantity.
And because the number of primes has been proven time and again to be infinite, as far back as 300BC,the Fibonacci primes MUST be finite.
QED.
If I've made a mistake, I'd like to know.11 -
So we have a course this semester called "Programming the web".
First lab:
Write a program using JS to take an int input using a alert box and then print it's multiplication table using ANOTHER ALERT BOX.
Yes, not even display on a page.
Next lab:
Print fibonacci numbers on a web page using JS. Because why not. Let's teach students JS how we taught them C and let's ignore the awesome stuff we can do with JS
Btw all this for a class that has never had a JS course and half the people don't even know what JS is. They just directly throw the program and are done with it.
I'm so gonna hate this semester1 -
What kind of a shitty interviewer asks Fibonacci series as the only one question in the last round ?6
-
Gonna teach someone conpletely new to programming some C#. What are some good exercises I can give them to understand general programming well?
So far I'm thinking FizzBuzz, some progressively more complex math+logic stuff and maybe fibonacci using recursion.11 -
At my company we have a rule that ticket estimates can only be pointed using numbers from the fibonacci series. So 4 point tickets are not allowed!
We’re also discouraged from giving an estimate larger than 5, and told that tickets need to be broken down into smaller tickets if we think it’s more than a 5.
Also, ticket estimates must include the full amount of time for dev, QA, AND deploy. Given how hard it is to work with our tech stack, few tasks actually fit.
All of this may sound fine in principle, but in practice it’s extremely frustrating. I’ve protested a few times but I’ve been told I’m outvoted and nobody wants to reconsider the decision that was made sometime in the distant past. I was also told that “most other companies do it this way”, so therefore we have to as well.
This is the first company I’ve ever worked at which had this stupid rule. Is it this way at your company? Is this a NorCal tech company thing? I’ve worked at several companies outside of the SV bubble, and never encountered this.6 -
Split everything into small tasks, no longer than two days of work
Use Fibonacci numbers, 1-2-3-5-8-13
A highly effective developer will produce about 80% of a work day. If you think a task is done within a day add 25% and your estimate is ten. Remember that we use Fibonacci and round up to 13.1 -
I was bored, spent an half hour writing a non-recursive, relatively-high-allocations, somewhat slow Fibonacci function.
Here you go: 15
15 -
Computer games is always been a on a great demand. As demand increases, production also increases. Gaming industry has been on a rise since the 19th century. The first computer game "Space Wars" in 1962 gained a large success. Since then, the evolution in the gaming industry is thrilling. Currently, we have access to many immersive games. With the introduction of AR and VR, the gaming industry is going to take a great burst in business. Don't you believe after decade the games would be so advanced that it would be so much life like. According to the predictions, after a hundred years, games would be vastly different from what we play today, realistic feature would be a sidekick for them. A time will come when the games would reach a singularity where the characters would have consciousness. Isn't that like our real world, as if we are the characters in a advanced game of some advanced beings. What if it is true? Scientists are doing a intensive research on this field to find a clue, whether we are in a game or not. This is the so called "Simulation Theory". Some clues in relation to this would be worth noting. The flower are following a series to have their petals. To be precise Fibonacci series is the base to the no of petals in a flower. (Fibonacci Series: 1 1 2 3 5 8 13 21 34 55.....) Flowers would either have 3 or 5 or 8 petals, but no flower is having a number of petal which is not following this series. Isn't it interesting, there is no brain in flower, even then how could a flower decide, how many petals it will contain? Sometimes, it feels like there is some kind of computer code is responsible for this. We will discuss about it furthur.15
-
I'm so over Fibonacci demos. It's become the Northwind database of algorithm examples.
Maybe a Rubik's Cube solver as a change of pace, perhaps?6 -
Who the fuck invented recursive😡, it sucks in numerical computation, it takes excessive amount of memory, recomputation and fffffffuck😡. To calculate fibonacci of 50, it feels like MARK I. fuck they do nothing more than calling, like Peter calling Peter...😡
 8
8 -
Building on yesterday's rant (https://devrant.com/rants/3110183/), after sleeping on it I realized that using groups was completely non-necessary, so I got rid of them and got a much more efficient (and faster) function:
Also, I've got these in a repo: https://github.com/chabad360/... 8
8 -
I want to print the first number in the Fibonacci sequence to contain over 1000 digits. I got fibbonaci to work but I cannot seem to figure out how to implement the "Contain over 1000 digits".
Do I make a list to store the fibbonaci numbers in then do a statement?
My Python 3 Code:
def fibonacci(num):
if num == 2 or num ==1:
return 1
return sum([fibonacci(num - 2), fibonacci(num - 1)])
print(fibonacci(7))6 -
So... Saying im an intermediate-beginner coder who had programming in highschool learning only Pascal, VB, VB+SQL and PHP coding something that i'll barely use in my developer career (programs like Fibonacci sequence and other math related stuff), can anyone give me some challenges in PHP/C#/Javascript simulating the "real programmers" actually code? Sorry for bad english3













